本文實例講述了Python3解決棋盤覆蓋問題的方法。分享給大家供大家參考,具體如下:
問題描述:
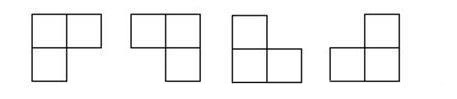
在2^k*2^k個方格組成的棋盤中,有一個方格被占用,用下圖的4種L型骨牌覆蓋所有棋盤上的其余所有方格,不能重疊。
代碼如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
def chess(tr,tc,pr,pc,size): global mark global table mark+=1 count=mark if size==1: return half=size//2 if pr<tr+half and pc<tc+half: chess(tr,tc,pr,pc,half) else: table[tr+half-1][tc+half-1]=count chess(tr,tc,tr+half-1,tc+half-1,half) if pr<tr+half and pc>=tc+half: chess(tr,tc+half,pr,pc,half) else: table[tr+half-1][tc+half]=count chess(tr,tc+half,tr+half-1,tc+half,half) if pr>=tr+half and pc<tc+half: chess(tr+half,tc,pr,pc,half) else: table[tr+half][tc+half-1]=count chess(tr+half,tc,tr+half,tc+half-1,half) if pr>=tr+half and pc>=tc+half: chess(tr+half,tc+half,pr,pc,half) else: table[tr+half][tc+half]=count chess(tr+half,tc+half,tr+half,tc+half,half)def show(table): n=len(table) for i in range(n): for j in range(n): print(table[i][j],end=' ') print('')mark=0n=8table=[[-1 for x in range(n)] for y in range(n)]chess(0,0,2,2,n)show(table) |
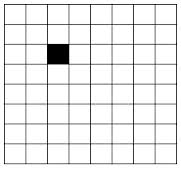
n是棋盤寬度,必須是2^k,本例中n=8,特殊格子在(2,2)位置,如下圖所示:
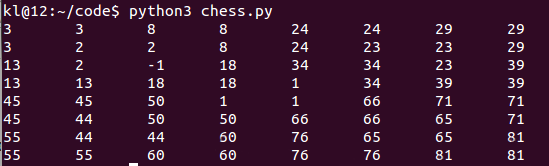
采用分治法每次把棋盤分成4份,如果特殊格子在這個小棋盤中則繼續分成4份,如果不在這個小棋盤中就把該小棋盤中靠近中央的那個格子置位,表示L型骨牌的1/3占據此處,每一次遞歸都會遍歷查詢4個小棋盤,三個不含有特殊格子的棋盤置位的3個格子正好在大棋盤中央構成一個完整的L型骨牌,依次類推,找到全部覆蓋方法。運行結果如下:
希望本文所述對大家Python程序設計有所幫助。
原文鏈接:http://blog.csdn.net/littlethunder/article/details/25288969