本筆記目的是通過tensorflow實現一個兩層的神經網絡。目的是實現一個二次函數的擬合。
如何添加一層網絡
代碼如下:
|
1
2
3
4
5
6
7
8
9
10
|
def add_layer(inputs, in_size, out_size, activation_function=None): # add one more layer and return the output of this layer Weights = tf.Variable(tf.random_normal([in_size, out_size])) biases = tf.Variable(tf.zeros([1, out_size]) + 0.1) Wx_plus_b = tf.matmul(inputs, Weights) + biases if activation_function is None: outputs = Wx_plus_b else: outputs = activation_function(Wx_plus_b) return outputs |
注意該函數中是xW+b,而不是Wx+b。所以要注意乘法的順序。x應該定義為[類別數量, 數據數量], W定義為[數據類別,類別數量]。
創建一些數據
|
1
2
3
4
|
# Make up some real datax_data = np.linspace(-1,1,300)[:, np.newaxis]noise = np.random.normal(0, 0.05, x_data.shape)y_data = np.square(x_data) - 0.5 + noise |
numpy的linspace函數能夠產生等差數列。start,stop決定等差數列的起止值。endpoint參數指定包不包括終點值。
|
1
2
3
|
numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)[source] Return evenly spaced numbers over a specified interval. Returns num evenly spaced samples, calculated over the interval [start, stop]. |

noise函數為添加噪聲所用,這樣二次函數的點不會與二次函數曲線完全重合。
numpy的newaxis可以新增一個維度而不需要重新創建相應的shape在賦值,非常方便,如上面的例子中就將x_data從一維變成了二維。
添加占位符,用作輸入
|
1
2
3
|
# define placeholder for inputs to networkxs = tf.placeholder(tf.float32, [None, 1])ys = tf.placeholder(tf.float32, [None, 1]) |
添加隱藏層和輸出層
|
1
2
3
4
|
# add hidden layerl1 = add_layer(xs, 1, 10, activation_function=tf.nn.relu)# add output layerprediction = add_layer(l1, 10, 1, activation_function=None) |
計算誤差,并用梯度下降使得誤差最小
|
1
2
3
|
# the error between prediciton and real dataloss = tf.reduce_mean(tf.reduce_sum(tf.square(ys - prediction),reduction_indices=[1]))train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss) |
完整代碼如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
from __future__ import print_functionimport tensorflow as tfimport numpy as npimport matplotlib.pyplot as pltdef add_layer(inputs, in_size, out_size, activation_function=None): # add one more layer and return the output of this layer Weights = tf.Variable(tf.random_normal([in_size, out_size])) biases = tf.Variable(tf.zeros([1, out_size]) + 0.1) Wx_plus_b = tf.matmul(inputs, Weights) + biases if activation_function is None: outputs = Wx_plus_b else: outputs = activation_function(Wx_plus_b) return outputs# Make up some real datax_data = np.linspace(-1,1,300)[:, np.newaxis]noise = np.random.normal(0, 0.05, x_data.shape)y_data = np.square(x_data) - 0.5 + noise# define placeholder for inputs to networkxs = tf.placeholder(tf.float32, [None, 1])ys = tf.placeholder(tf.float32, [None, 1])# add hidden layerl1 = add_layer(xs, 1, 10, activation_function=tf.nn.relu)# add output layerprediction = add_layer(l1, 10, 1, activation_function=None)# the error between prediciton and real dataloss = tf.reduce_mean(tf.reduce_sum(tf.square(ys - prediction), reduction_indices=[1]))train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss)# important stepinit = tf.initialize_all_variables()sess = tf.Session()sess.run(init)# plot the real datafig = plt.figure()ax = fig.add_subplot(1,1,1)ax.scatter(x_data, y_data)plt.ion()plt.show()for i in range(1000): # training sess.run(train_step, feed_dict={xs: x_data, ys: y_data}) if i % 50 == 0: # to visualize the result and improvement try: ax.lines.remove(lines[0]) except Exception: pass prediction_value = sess.run(prediction, feed_dict={xs: x_data}) # plot the prediction lines = ax.plot(x_data, prediction_value, 'r-', lw=5) plt.pause(0.1) |
運行結果:
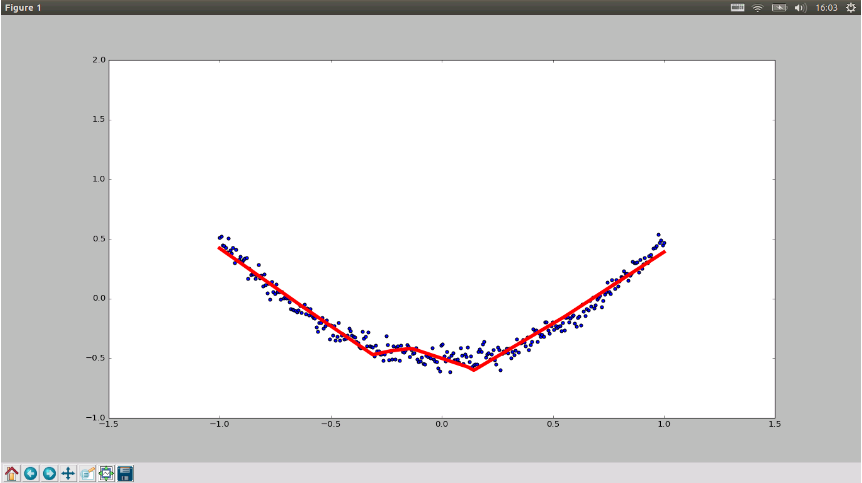
以上就是本文的全部內容,希望對大家的學習有所幫助,也希望大家多多支持服務器之家。
原文鏈接:http://blog.csdn.net/qq_30159351/article/details/52639291