本文實例講述了Python實現(xiàn)將n個點均勻地分布在球面上的方法。分享給大家供大家參考。具體分析如下：

最近工作上遇到一個需求，將10000左右個點均勻地分布在一個球面上。所謂的均勻，即相鄰的兩個點之間的距離盡量一致。

我的算法是用基于正多面體剖分球面，我選的是正八面體。

1. 效果圖如下：

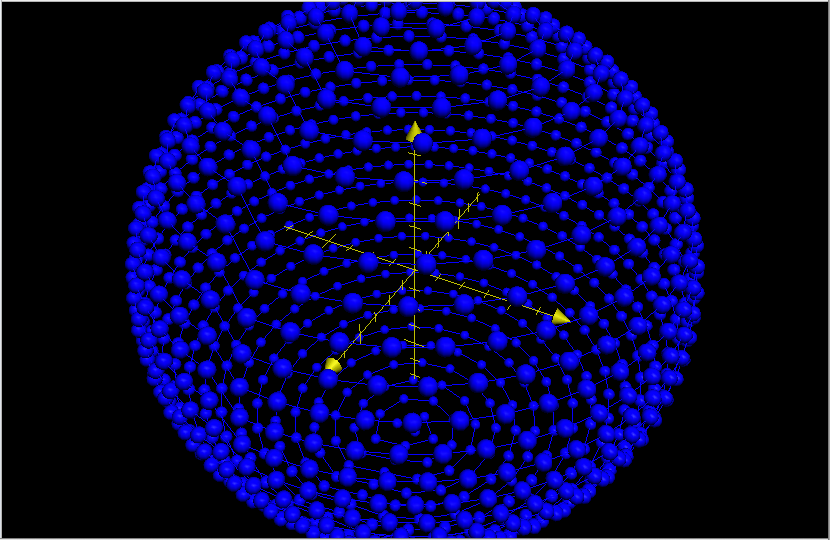
2.sphere.py代碼如下

1. #!/usr/bin/python 
2. # -*- coding: utf-8 -*- 
3. import math 
4. class Spherical(object): 
5.   '''球坐標系''' 
6.   def __init__(self, radial = 1.0, polar = 0.0, azimuthal = 0.0): 
7.     self.radial = radial 
8.     self.polar = polar 
9.     self.azimuthal = azimuthal 
10.   def toCartesian(self): 
11.     '''轉(zhuǎn)直角坐標系''' 
12.     r = math.sin(self.azimuthal) * self.radial 
13.     x = math.cos(self.polar) * r 
14.     y = math.sin(self.polar) * r 
15.     z = math.cos(self.azimuthal) * self.radial 
16.     return x, y, z 
17. def splot(limit): 
18.   s = Spherical() 
19.   n = int(math.ceil(math.sqrt((limit - 2) / 4))) 
20.   azimuthal = 0.5 * math.pi / n 
21.   for a in range(-n, n + 1): 
22.     s.polar = 0 
23.     size = (n - abs(a)) * 4 or 1 
24.     polar = 2 * math.pi / size 
25.     for i in range(size): 
26.       yield s.toCartesian() 
27.       s.polar += polar 
28.     s.azimuthal += azimuthal 
29. for point in splot(input('')): 
30.   print("%f %f %f" % point) 

希望本文所述對大家的Python程序設計有所幫助。