本文實例講述了java數(shù)據(jù)結(jié)構(gòu)與算法之桶排序?qū)崿F(xiàn)方法。分享給大家供大家參考,具體如下:
基本思想:
假定輸入是由一個隨機過程產(chǎn)生的[0, M)區(qū)間上均勻分布的實數(shù)。將區(qū)間[0, M)劃分為n個大小相等的子區(qū)間(桶),將n個輸入元素分配到這些桶中,對桶中元素進行排序,然后依次連接桶輸入0 ≤A[1..n] <M輔助數(shù)組B[0..n-1]是一指針數(shù)組,指向桶(鏈表)。將n個記錄分布到各個桶中去。如果有多于一個記錄分到同一個桶中,需要進行桶內(nèi)排序。最后依次把各個桶中的記錄列出來記得到有序序列。
[桶——關(guān)鍵字]映射函數(shù)
bindex=f(key) 其中,bindex 為桶數(shù)組B的下標(即第bindex個桶), k為待排序列的關(guān)鍵字。桶排序之所以能夠高效,其關(guān)鍵在于這個映射函數(shù),它必須做到:如果關(guān)鍵字k1<k2,那么f(k1)<=f(k2)。也就是說B(i)中的最大數(shù)據(jù)都要小于B(i+1)中最小數(shù)據(jù)。很顯然,映射函數(shù)的確定與數(shù)據(jù)本身的特點有很大的關(guān)系,我們下面舉個例子:
假如待排序列K= {49、 38 、 35、 97 、 76、 73 、 27、 49 }。這些數(shù)據(jù)全部在1—100之間。因此我們定制10個桶,然后確定映射函數(shù)f(k)=k/10。則第一個關(guān)鍵字49將定位到第4個桶中(49/10=4)。依次將所有關(guān)鍵字全部堆入桶中,并在每個非空的桶中進行快速排序后得到如下圖所示:
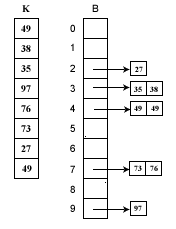
對上圖只要順序輸出每個B[i]中的數(shù)據(jù)就可以得到有序序列了。
算法核心代碼如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
/// <summary>/// 桶排序//////如果有重復的數(shù)字,則需要 List<int>數(shù)組,這里舉的例子沒有重復的數(shù)字/// </summary>/// <param name="unsorted">待排數(shù)組</param>/// <param name="maxNumber">待排數(shù)組中的最大數(shù),如果可以提供的話</param>/// <returns></returns>static int[] bucket_sort(int[] unsorted, int maxNumber = 97){ int[] sorted = new int[maxNumber + 1]; for (int i = 0; i < unsorted.Length; i++) { sorted[unsorted[i]] = unsorted[i]; } return sorted;}static void Main(string[] args){ int[] x = {49、 38 、 35、 97 、 76、 73 、 27、 49 }; var sorted = bucket_sort(x, 97); for (int i = 0; i < sorted.Length; i++) { if (sorted[i] > 0) Console.WriteLine(sorted[i]); } Console.ReadLine();} |
桶排序代價分析
桶排序利用函數(shù)的映射關(guān)系,減少了幾乎所有的比較工作。實際上,桶排序的f(k)值的計算,其作用就相當于快排中劃分,已經(jīng)把大量數(shù)據(jù)分割成了基本有序的數(shù)據(jù)塊(桶)。然后只需要對桶中的少量數(shù)據(jù)做先進的比較排序即可。
對N個關(guān)鍵字進行桶排序的時間復雜度分為兩個部分:
(1) 循環(huán)計算每個關(guān)鍵字的桶映射函數(shù),這個時間復雜度是O(N)。
(2) 利用先進的比較排序算法對每個桶內(nèi)的所有數(shù)據(jù)進行排序,其時間復雜度為 ∑ O(Ni*logNi) 。其中Ni 為第i個桶的數(shù)據(jù)量。
很顯然,第(2)部分是桶排序性能好壞的決定因素。盡量減少桶內(nèi)數(shù)據(jù)的數(shù)量是提高效率的唯一辦法(因為基于比較排序的最好平均時間復雜度只能達到O(N*logN)了)。因此,我們需要盡量做到下面兩點:
(1) 映射函數(shù)f(k)能夠?qū)個數(shù)據(jù)平均的分配到M個桶中,這樣每個桶就有[N/M]個數(shù)據(jù)量。
(2) 盡量的增大桶的數(shù)量。極限情況下每個桶只能得到一個數(shù)據(jù),這樣就完全避開了桶內(nèi)數(shù)據(jù)的“比較”排序操作。當然,做到這一點很不容易,數(shù)據(jù)量巨大的情況下,f(k)函數(shù)會使得桶集合的數(shù)量巨大,空間浪費嚴重。這就是一個時間代價和空間代價的權(quán)衡問題了。
對于N個待排數(shù)據(jù),M個桶,平均每個桶[N/M]個數(shù)據(jù)的桶排序平均時間復雜度為:
O(N)+O(M*(N/M)*log(N/M))=O(N+N*(logN-logM))=O(N+N*logN-N*logM)
當N=M時,即極限情況下每個桶只有一個數(shù)據(jù)時。桶排序的最好效率能夠達到O(N)。
總結(jié): 桶排序的平均時間復雜度為線性的O(N+C),其中C=N*(logN-logM)。如果相對于同樣的N,桶數(shù)量M越大,其效率越高,最好的時間復雜度達到O(N)。 當然桶排序的空間復雜度 為O(N+M),如果輸入數(shù)據(jù)非常龐大,而桶的數(shù)量也非常多,則空間代價無疑是昂貴的。此外,桶排序是穩(wěn)定的。
即以下三點:
1. 桶排序是穩(wěn)定的
2. 桶排序是常見排序里最快的一種,比快排還要快…大多數(shù)情況下
3. 桶排序非常快,但是同時也非常耗空間,基本上是最耗空間的一種排序算法
補充:在查找算法中,基于比較的查找算法最好的時間復雜度也是O(logN)。比如折半查找、平衡二叉樹、紅黑樹等。但是Hash表卻有O(C)線性級別的查找效率(不沖突情況下查找效率達到O(1))。那么:Hash表的思想和桶排序是不是有一曲同工之妙呢?
實際上,桶排序?qū)?shù)據(jù)的條件有特殊要求,如果數(shù)組很大的話,那么分配幾億個桶顯然是不可能的。所以桶排序有其局限性,適合元素值集合并不大的情況。
希望本文所述對大家java程序設(shè)計有所幫助。