預(yù)備知識

堆排序

堆排序是利用堆這種數(shù)據(jù)結(jié)構(gòu)而設(shè)計(jì)的一種排序算法，堆排序是一種選擇排序，它的最壞，最好，平均時(shí)間復(fù)雜度均為O(nlogn)，它也是不穩(wěn)定排序。首先簡單了解下堆結(jié)構(gòu)。

堆

堆是具有以下性質(zhì)的完全二叉樹：每個(gè)結(jié)點(diǎn)的值都大于或等于其左右孩子結(jié)點(diǎn)的值，稱為大頂堆；或者每個(gè)結(jié)點(diǎn)的值都小于或等于其左右孩子結(jié)點(diǎn)的值，稱為小頂堆。如下圖：

圖解Java排序算法之堆排序

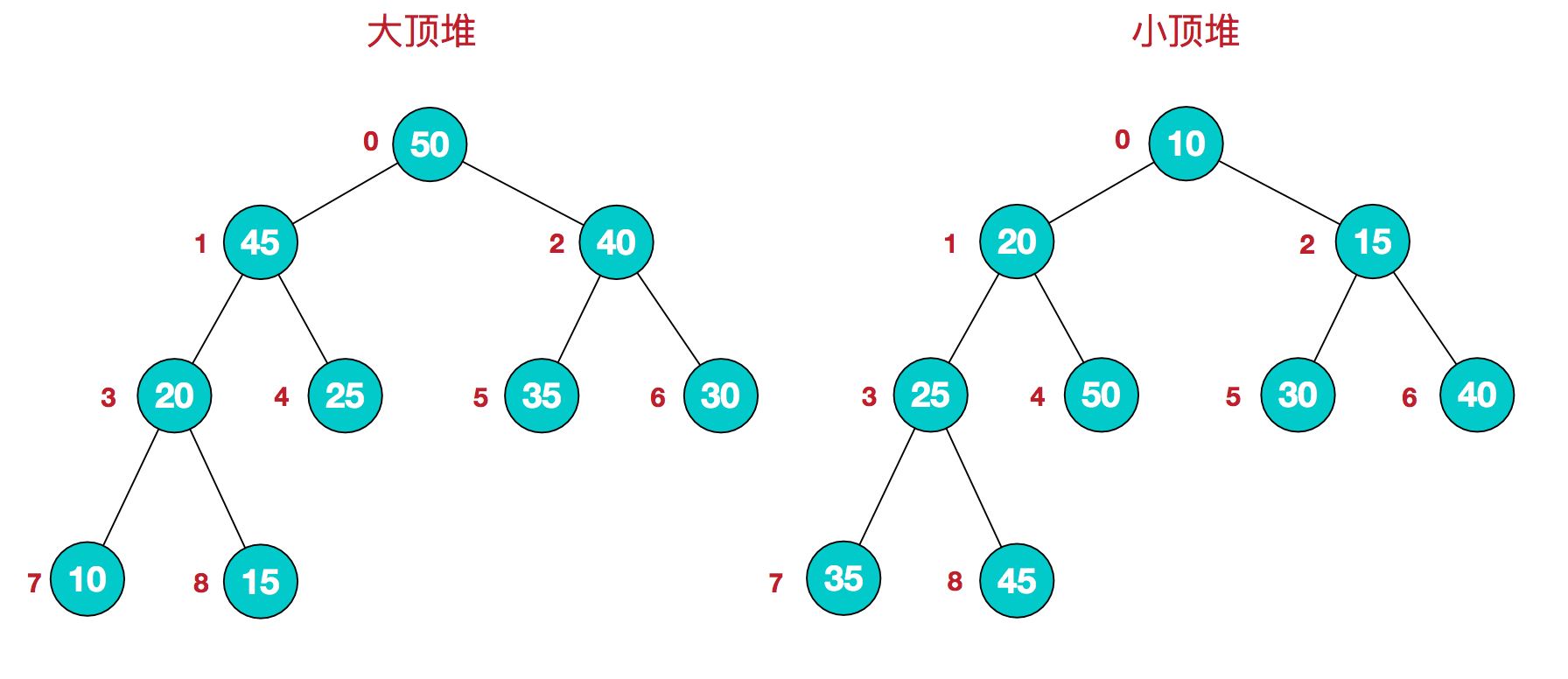
同時(shí)，我們對堆中的結(jié)點(diǎn)按層進(jìn)行編號，將這種邏輯結(jié)構(gòu)映射到數(shù)組中就是下面這個(gè)樣子

圖解Java排序算法之堆排序

該數(shù)組從邏輯上講就是一個(gè)堆結(jié)構(gòu)，我們用簡單的公式來描述一下堆的定義就是：

大頂堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]

小頂堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

ok，了解了這些定義。接下來，我們來看看堆排序的基本思想及基本步驟：

圖解Java堆排序算法

堆排序基本思想及步驟

　　堆排序的基本思想是：將待排序序列構(gòu)造成一個(gè)大頂堆，此時(shí)，整個(gè)序列的最大值就是堆頂?shù)母?jié)點(diǎn)。將其與末尾元素進(jìn)行交換，此時(shí)末尾就為最大值。然后將剩余n-1個(gè)元素重新構(gòu)造成一個(gè)堆，這樣會(huì)得到n個(gè)元素的次小值。如此反復(fù)執(zhí)行，便能得到一個(gè)有序序列了

步驟一.構(gòu)造初始堆。將給定無序序列構(gòu)造成一個(gè)大頂堆（一般升序采用大頂堆，降序采用小頂堆)。

a.假設(shè)給定無序序列結(jié)構(gòu)如下

圖解Java排序算法之堆排序

1.此時(shí)我們從最后一個(gè)非葉子結(jié)點(diǎn)開始（葉結(jié)點(diǎn)自然不用調(diào)整，第一個(gè)非葉子結(jié)點(diǎn) arr.length/2-1=5/2-1=1，也就是下面的6結(jié)點(diǎn)），從左至右，從下至上進(jìn)行調(diào)整。

圖解Java排序算法之堆排序

2.找到第二個(gè)非葉節(jié)點(diǎn)4，由于[4,9,8]中9元素最大，4和9交換。

圖解Java排序算法之堆排序

這時(shí)，交換導(dǎo)致了子根[4,5,6]結(jié)構(gòu)混亂，繼續(xù)調(diào)整，[4,5,6]中6最大，交換4和6。

圖解Java排序算法之堆排序

此時(shí)，我們就將一個(gè)無需序列構(gòu)造成了一個(gè)大頂堆。

步驟二. 將堆頂元素與末尾元素進(jìn)行交換，使末尾元素最大。然后繼續(xù)調(diào)整堆，再將堆頂元素與末尾元素交換，得到第二大元素。如此反復(fù)進(jìn)行交換、重建、交換。

a.將堆頂元素9和末尾元素4進(jìn)行交換

圖解Java排序算法之堆排序

b.重新調(diào)整結(jié)構(gòu)，使其繼續(xù)滿足堆定義

圖解Java排序算法之堆排序

c.再將堆頂元素8與末尾元素5進(jìn)行交換，得到第二大元素8.

圖解Java排序算法之堆排序

后續(xù)過程，繼續(xù)進(jìn)行調(diào)整，交換，如此反復(fù)進(jìn)行，最終使得整個(gè)序列有序

圖解Java排序算法之堆排序

再簡單總結(jié)下堆排序的基本思路：

a.將無需序列構(gòu)建成一個(gè)堆，根據(jù)升序降序需求選擇大頂堆或小頂堆;

b.將堆頂元素與末尾元素交換，將最大元素"沉"到數(shù)組末端;

c.重新調(diào)整結(jié)構(gòu)，使其滿足堆定義，然后繼續(xù)交換堆頂元素與當(dāng)前末尾元素，反復(fù)執(zhí)行調(diào)整+交換步驟，直到整個(gè)序列有序。

圖解Java堆排序算法

代碼實(shí)現(xiàn)

package sortdemo;
import java.util.Arrays;
/**
* Created by chengxiao on 2016/12/17.
* 堆排序demo
*/
public class HeapSort {
  public static void main(String []args){
      int []arr = {9,8,7,6,5,4,3,2,1};
      sort(arr);
      System.out.println(Arrays.toString(arr));
  }
  public static void sort(int []arr){
      //1.構(gòu)建大頂堆
      for(int i=arr.length/2-1;i>=0;i--){
          //從第一個(gè)非葉子結(jié)點(diǎn)從下至上，從右至左調(diào)整結(jié)構(gòu)
          adjustHeap(arr,i,arr.length);
      }
      //2.調(diào)整堆結(jié)構(gòu)+交換堆頂元素與末尾元素
      for(int j=arr.length-1;j>0;j--){
          swap(arr,0,j);//將堆頂元素與末尾元素進(jìn)行交換
          adjustHeap(arr,0,j);//重新對堆進(jìn)行調(diào)整
      }
  }
  /**
   * 調(diào)整大頂堆（僅是調(diào)整過程，建立在大頂堆已構(gòu)建的基礎(chǔ)上）
   * @param arr
   * @param i
   * @param length
   */
  public static void adjustHeap(int []arr,int i,int length){
      int temp = arr[i];//先取出當(dāng)前元素i
      for(int k=i*2+1;k<length;k=k*2+1){//從i結(jié)點(diǎn)的左子結(jié)點(diǎn)開始，也就是2i+1處開始
          if(k+1<length && arr[k]<arr[k+1]){//如果左子結(jié)點(diǎn)小于右子結(jié)點(diǎn)，k指向右子結(jié)點(diǎn)
              k++;
          }
          if(arr[k] >temp){//如果子節(jié)點(diǎn)大于父節(jié)點(diǎn)，將子節(jié)點(diǎn)值賦給父節(jié)點(diǎn)（不用進(jìn)行交換）
              arr[i] = arr[k];
              i = k;
          }else{
              break;
          }
      }
      arr[i] = temp;//將temp值放到最終的位置
  }
  /**
   * 交換元素
   * @param arr
   * @param a
   * @param b
   */
  public static void swap(int []arr,int a ,int b){
      int temp=arr[a];
      arr[a] = arr[b];
      arr[b] = temp;
  }
}

結(jié)果

[1, 2, 3, 4, 5, 6, 7, 8, 9]

總結(jié)

堆排序是一種選擇排序，整體主要由構(gòu)建初始堆+交換堆頂元素和末尾元素并重建堆兩部分組成。其中構(gòu)建初始堆經(jīng)推導(dǎo)復(fù)雜度為O(n)，在交換并重建堆的過程中，需交換n-1次，而重建堆的過程中，根據(jù)完全二叉樹的性質(zhì)，[log2(n-1),log2(n-2)...1]逐步遞減，近似為nlogn。所以堆排序時(shí)間復(fù)雜度一般認(rèn)為就是O(nlogn)級。

本篇文章就到這里了，希望能夠給你帶來幫助，也希望您能夠多多關(guān)注服務(wù)器之家的更多內(nèi)容!

原文鏈接：https://www.cnblogs.com/chengxiao/p/6129630.html