想當(dāng)初,考研的時候要是知道有這么個好東西,計算定積分。。。開玩笑,那時候計算定積分根本沒有這么簡單的。但這確實給我打開了一種思路,用編程語言去解決更多更復(fù)雜的數(shù)學(xué)問題。下面進(jìn)入正題。

如上圖所示,計算區(qū)間[a b]上f(x)的積分即求曲線與X軸圍成紅色區(qū)域的面積。下面使用蒙特卡洛法計算區(qū)間[2 3]上的定積分:∫(x2+4*x*sin(x))dx
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
# -*- coding: utf-8 -*-import numpy as npimport matplotlib.pyplot as pltdef f(x): return x**2 + 4*x*np.sin(x) def intf(x): return x**3/3.0+4.0*np.sin(x) - 4.0*x*np.cos(x)a = 2; b = 3; # use N draws N= 10000X = np.random.uniform(low=a, high=b, size=N) # N values uniformly drawn from a to b Y =f(X) # CALCULATE THE f(x) # 蒙特卡洛法計算定積分:面積=寬度*平均高度Imc= (b-a) * np.sum(Y)/ N;exactval=intf(b)-intf(a)print "Monte Carlo estimation=",Imc, "Exact number=", intf(b)-intf(a)# --How does the accuracy depends on the number of points(samples)? Lets try the same 1-D integral # The Monte Carlo methods yield approximate answers whose accuracy depends on the number of draws.Imc=np.zeros(1000)Na = np.linspace(0,1000,1000)exactval= intf(b)-intf(a)for N in np.arange(0,1000): X = np.random.uniform(low=a, high=b, size=N) # N values uniformly drawn from a to b Y =f(X) # CALCULATE THE f(x) Imc[N]= (b-a) * np.sum(Y)/ N; plt.plot(Na[10:],np.sqrt((Imc[10:]-exactval)**2), alpha=0.7)plt.plot(Na[10:], 1/np.sqrt(Na[10:]), 'r')plt.xlabel("N")plt.ylabel("sqrt((Imc-ExactValue)$^2$)")plt.show() |
>>>
Monte Carlo estimation= 11.8181144118 Exact number= 11.8113589251
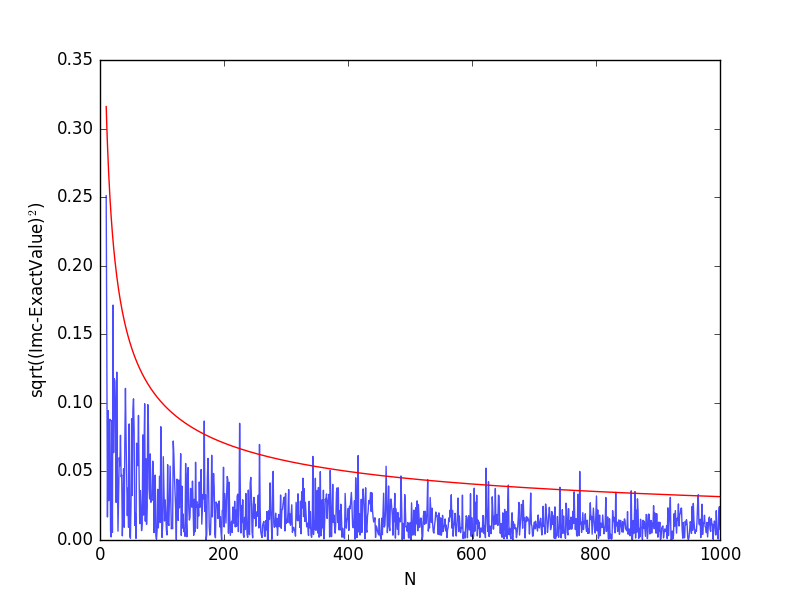
從上圖可以看出,隨著采樣點數(shù)的增加,計算誤差逐漸減小。想要提高模擬結(jié)果的精確度有兩個途徑:其一是增加試驗次數(shù)N;其二是降低方差σ2. 增加試驗次數(shù)勢必使解題所用計算機的總時間增加,要想以此來達(dá)到提高精度之目的顯然是不合適的。下面來介紹重要抽樣法來減小方差,提高積分計算的精度。
重要性抽樣法的特點在于,它不是從給定的過程的概率分布抽樣,而是從修改的概率分布抽樣,使對模擬結(jié)果有重要作用的事件更多出現(xiàn),從而提高抽樣效率,減少花費在對模擬結(jié)果無關(guān)緊要的事件上的計算時間。比如在區(qū)間[a b]上求g(x)的積分,若采用均勻抽樣,在函數(shù)值g(x)比較小的區(qū)間內(nèi)產(chǎn)生的抽樣點跟函數(shù)值較大處區(qū)間內(nèi)產(chǎn)生的抽樣點的數(shù)目接近,顯然抽樣效率不高,可以將抽樣概率密度函數(shù)改為f(x),使f(x)與g(x)的形狀相近,就可以保證對積分計算貢獻(xiàn)較大的抽樣值出現(xiàn)的機會大于貢獻(xiàn)小的抽樣值,即可以將積分運算改寫為:

x是按照概率密度f(x)抽樣獲得的隨機變量,顯然在區(qū)間[a b]內(nèi)應(yīng)該有:

因此,可容易將積分值I看成是隨機變量 Y = g(x)/f(x)的期望,式子中xi是服從概率密度f(x)的采樣點

下面的例子采用一個正態(tài)分布函數(shù)f(x)來近似g(x)=sin(x)*x,并依據(jù)正態(tài)分布選取采樣值計算區(qū)間[0 pi]上的積分個∫g(x)dx
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
|
# -*- coding: utf-8 -*-# Example: Calculate ∫sin(x)xdx# The function has a shape that is similar to Gaussian and therefore# we choose here a Gaussian as importance sampling distribution.from scipy import statsfrom scipy.stats import normimport numpy as npimport matplotlib.pyplot as pltmu = 2;sig =.7;f = lambda x: np.sin(x)*xinfun = lambda x: np.sin(x)-x*np.cos(x)p = lambda x: (1/np.sqrt(2*np.pi*sig**2))*np.exp(-(x-mu)**2/(2.0*sig**2))normfun = lambda x: norm.cdf(x-mu, scale=sig)plt.figure(figsize=(18,8)) # set the figure size# range of integrationxmax =np.pi xmin =0# Number of draws N =1000# Just want to plot the functionx=np.linspace(xmin, xmax, 1000)plt.subplot(1,2,1)plt.plot(x, f(x), 'b', label=u'Original $x\sin(x)$')plt.plot(x, p(x), 'r', label=u'Importance Sampling Function: Normal')plt.xlabel('x')plt.legend()# =============================================# EXACT SOLUTION # =============================================Iexact = infun(xmax)-infun(xmin)print Iexact# ============================================# VANILLA MONTE CARLO # ============================================Ivmc = np.zeros(1000)for k in np.arange(0,1000): x = np.random.uniform(low=xmin, high=xmax, size=N) Ivmc[k] = (xmax-xmin)*np.mean(f(x))# ============================================# IMPORTANCE SAMPLING # ============================================# CHOOSE Gaussian so it similar to the original functions# Importance sampling: choose the random points so that# more points are chosen around the peak, less where the integrand is small.Iis = np.zeros(1000)for k in np.arange(0,1000): # DRAW FROM THE GAUSSIAN: xis~N(mu,sig^2) xis = mu + sig*np.random.randn(N,1); xis = xis[ (xis<xmax) & (xis>xmin)] ; # normalization for gaussian from 0..pi normal = normfun(np.pi)-normfun(0) # 注意:概率密度函數(shù)在采樣區(qū)間[0 pi]上的積分需要等于1 Iis[k] =np.mean(f(xis)/p(xis))*normal # 因此,此處需要乘一個系數(shù)即p(x)在[0 pi]上的積分plt.subplot(1,2,2)plt.hist(Iis,30, histtype='step', label=u'Importance Sampling');plt.hist(Ivmc, 30, color='r',histtype='step', label=u'Vanilla MC');plt.vlines(np.pi, 0, 100, color='g', linestyle='dashed')plt.legend()plt.show() |
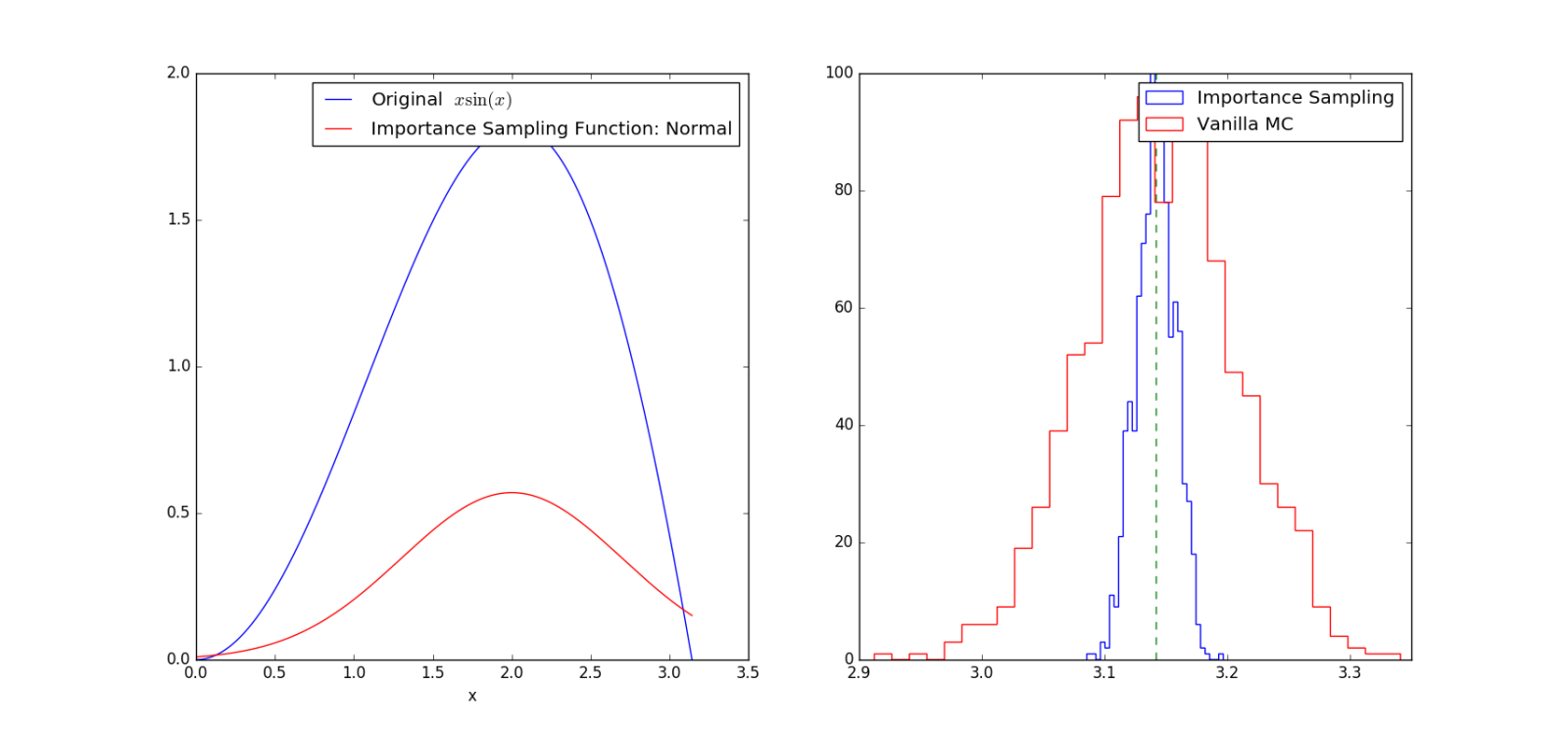
從圖中可以看出曲線sin(x)*x的形狀和正態(tài)分布曲線的形狀相近,因此在曲線峰值處的采樣點數(shù)目會比曲線上位置低的地方要多。精確計算的結(jié)果為pi,從上面的右圖中可以看出:兩種方法均計算定積分1000次,靠近精確值pi=3.1415處的結(jié)果最多,離精確值越遠(yuǎn)數(shù)目越少,顯然這符合常規(guī)。但是采用傳統(tǒng)方法(紅色直方圖)計算出的積分值方的差明顯比采用重要抽樣法(藍(lán)色直方圖)要大。因此,采用重要抽樣法計算可以降低方差,提高精度。另外需要注意的是:關(guān)于函數(shù)f(x)的選擇會對計算結(jié)果的精度產(chǎn)生影響,當(dāng)我們選擇的函數(shù)f(x)與g(x)相差較大時,計算結(jié)果的方差也會加大。
總結(jié)
以上就是本文關(guān)于python編程通過蒙特卡洛法計算定積分詳解的全部內(nèi)容,希望對大家有所幫助。如有不足之處,歡迎留言指出。感謝朋友們對本站的支持!
原文鏈接:http://www.cnblogs.com/21207-iHome/p/5269191.html