二叉堆是一種特殊的堆,二叉堆是完全二元樹(二叉樹)或者是近似完全二元樹(二叉樹)。二叉堆有兩種:最大堆和最小堆。最大堆:父結點的鍵值總是大于或等于任何一個子節點的鍵值;最小堆:父結點的鍵值總是小于或等于任何一個子節點的鍵值。
打印二叉堆:利用層級關系
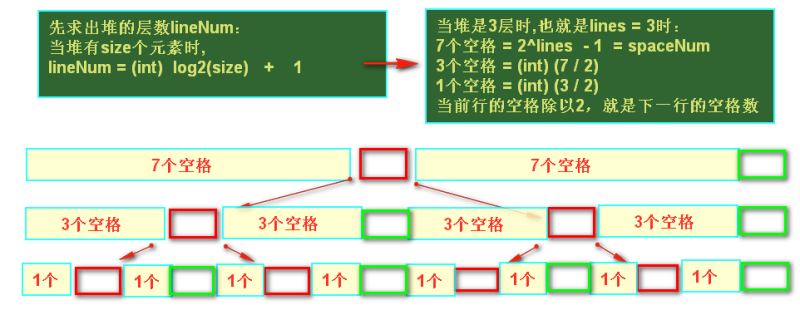
我這里是先將堆排序,然后在sort里執行了打印堆的方法printastree()
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
|
public class maxheap<t extends comparable<? super t>> { private t[] data; private int size; private int capacity; public maxheap(int capacity) { this.capacity = capacity; this.size = 0; this.data = (t[]) new comparable[capacity + 1]; } public maxheap(t[] arr) {//heapify,數組建堆 capacity = arr.length; data = (t[]) new comparable[capacity + 1]; system.arraycopy(arr, 0, data, 1, arr.length); size = arr.length; for (int i = size / 2; i >= 1; i--) { shiftdown(i); } } public int size() { return this.size; } public int getcapacity() { return this.capacity; } public boolean isempty() { return size == 0; } public t seekmax() { return data[1]; } public void swap(int i, int j) { if (i != j) { t temp = data[i]; data[i] = data[j]; data[j] = temp; } } public void insert(t item) { size++; data[size] = item; shiftup(size); } public t popmax() { swap(1, size--); shiftdown(1); return data[size + 1]; } public void shiftup(int child) { while (child > 1 && data[child].compareto(data[child / 2]) > 0) { swap(child, child / 2); child /= 2; } } /** * @param a data數組中某個元素的下角標 * @param b data數組中某個元素的下角標 * @return 哪個元素大就返回哪個的下角標 */ private int max(int a, int b) { if (data[a].compareto(data[b]) < 0) {//如果data[b]大 return b;//返回b } else {//如果data[a]大 return a;//返回a } } /** * @param a data數組中某個元素的下角標 * @param b data數組中某個元素的下角標 * @param c data數組中某個元素的下角標 * @return 哪個元素大就返回哪個的下角標 */ private int max(int a, int b, int c) { int biggest = max(a, b); biggest = max(biggest, c); return biggest; } public void shiftdown(int father) { while (true) { int lchild = father * 2; int rchild = father * 2 + 1; int newfather = father;//這里賦不賦值無所謂,如果把下面這個return改成break,那就必須賦值了 if (lchild > size) {//如果沒有左、右孩子 return; } else if (rchild > size) {//如果沒有右孩子 newfather = max(father, lchild); } else {//如果有左、右孩子 newfather = max(father, lchild, rchild); } if (newfather == father) {//如果原父結點就是三者最大,則不用繼續整理堆了 return; } else {//父節點不是最大,則把大的孩子交換上來,然后繼續往下堆調整,直到滿足大根堆為止 swap(newfather, father); father = newfather;//相當于繼續shiftdown(newfather)。假如newfather原來是father的左孩子,那就相當于shiftdown(2*father) } } } public static <t extends comparable<? super t>> void sort(t[] arr) { int len = arr.length; maxheap<t> maxheap = new maxheap<>(arr); maxheap.printastree(); for (int i = len - 1; i >= 0; i--) { arr[i] = maxheap.popmax(); } } public static void printarr(object[] arr) { for (object o : arr) { system.out.print(o); system.out.print("\t"); } system.out.println(); } public void printspace(int n) {//打印n個空格(在這里用‘\t'來代替) for (int i = 0; i < n; i++) { system.out.printf("%3s", ""); } } public void printastree() { int linenum = 1;//首先遍歷第一行 int lines = (int) (math.log(size) / math.log(2)) + 1;//lines是堆的層數 int spacenum = (int) (math.pow(2, lines) - 1); for (int i = 1; i <= size; ) { //因為在[1...size]左閉右閉區間存數據,data[0]不存數據 //每層都是打印這個區間[2^(層數-1) ... (2^層數)-1]。如果堆里的數不夠(2^層數)-1個,那就打印到size。所以取min((2^層數)-1,size). for (int j = (int) math.pow(2, linenum - 1); j <= math.min(size, (int) math.pow(2, linenum) - 1); j++) { printspace(spacenum); //打印spacenum個空格 system.out.printf("%3s", data[j]);//打印數據 system.out.printf("%3s", "");//圖片中綠色方框 printspace(spacenum);//打印spacenum個空格 i++;//每打印一個元素就 + 1 } linenum++; spacenum = spacenum / 2; system.out.println(); } } public static void main(string args[]) { integer[] arr = {3, 5, 1, 7, 2, 9, 8, 0, 4, 6, 1, 3, 6, 1, 1}; sort(arr); }} |
執行結果:

總結
以上就是本文關于java語言實現二叉堆的打印代碼分享的全部內容,希望對大家有所幫助。感興趣的朋友可以繼續參閱本站其他相關專題,如有不足之處,歡迎留言指出。感謝朋友們對本站的支持!
原文鏈接:http://www.cnblogs.com/noKing/p/7966272.html