平衡二叉樹:
在上一節二叉樹的基礎上我們實現,如何將生成平衡的二叉樹
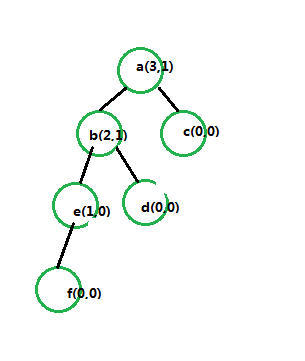
所謂平衡二叉樹:
我自己定義就是:任何一個節點的左高度和右高度的差的絕對值都小于2
如圖所示,此時a的左高度等于3,有高度等于1,差值為2,屬于不平衡中的左偏
此時的處理辦法就是:
將不平衡的元素的左枝的最右節點變為當前節點,
此時分兩種情況:
一、左枝有最右節點
將最右節點的左枝賦予其父節點的右枝
二、左枝沒有最右節點,
直接將左枝節點做父級節點,父級節點做其右枝
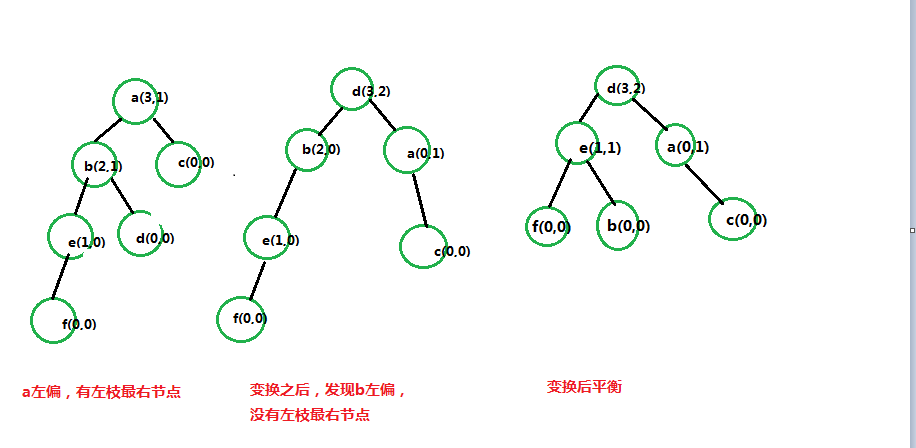
如圖所示,圖更清楚些。
可能會有疑問,為什么這樣變換?
假定a左偏,就需要一個比a小的最少一個值d(因為d唯一 一個是比a小,而且比a的左枝所有數都大的值)做父集結點,a做d的右枝,這樣在最上面的d節點就平衡了。
我們可以反證一下:
如果不是d是另一個數假設為h,此時h做父節點,a做父節點的右節點
因為a在h右邊,所以 a > h
因為b,e,d,f都是h的左枝,所以 h>d>b>e>f
所以 a>h>d>b>e>f
所以在不加入新節點的情況下,就只能是d
左偏和右偏是一樣的,可以完全鏡像過來就ok了
處理了所有節點 的左偏和右偏使整個二叉樹平衡,這就是平衡二叉樹的基本思想
代碼實現:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
|
# -*- coding:utf-8 -*-# 日期:2018/6/12 8:37# author:小鼠標# 節點對象class node: def __init__(self): self.left_children = none self.left_height = 0 self.right_children = none self.right_height = 0 self.value = none# 二叉樹對象class tree: def __init__(self): self.root = false self.front_list = [] self.middle_list = [] self.after_list = [] # 生成二叉樹 def create_tree(self,n=0,l=[]): if l == []: print("傳入的列表為空") return if n > len(l)-1: print("二叉樹生成") return node = node() node.value = l[n] if not self.root: self.root = node self.list = l else: self.add(self.root,node) self.create_tree(n+1,l) # 添加節點 def add(self,parent,new_node): if new_node.value > parent.value: # 插入值比父親值大,所以在父節點右邊 if parent.right_children == none: parent.right_children = new_node # 新插入節點的父親節點的高度值為1,也就是子高度值0+1 parent.right_height = 1 # 插入值后 從下到上更新節點的height else: self.add(parent.right_children,new_node) # 父親節點的右高度等于右孩子,左右高度中較大的值 + 1 parent.right_height = max(parent.right_children.right_height, parent.right_children.left_height) + 1 # ======= 此處開始判斷平衡二叉樹======= # 右邊高度大于左邊高度 屬于右偏 if parent.right_height - parent.left_height >= 2: self.right_avertence(parent) else: # 插入值比父親值小,所以在父節點左邊 if parent.left_children == none: parent.left_children = new_node parent.left_height = 1 else: self.add(parent.left_children,new_node) parent.left_height = max(parent.left_children.right_height, parent.left_children.left_height) + 1 # ======= 此處開始判斷平衡二叉樹======= # 左邊高度大于右邊高度 屬于左偏 if parent.left_height - parent.right_height >= 2: self.left_avertence(parent) # 更新當前節點下的所有節點的高度 def update_height(self,node): # 初始化節點高度值為0 node.left_height = 0 node.right_height = 0 # 是否到最底層的一個 if node.left_children == none and node.right_children == none: return else: if node.left_children: self.update_height(node.left_children) # 當前節點的高度等于左右子節點高度的較大值 + 1 node.left_height = max(node.left_children.left_height,node.left_children.right_height) + 1 if node.right_children: self.update_height(node.right_children) # 當前節點的高度等于左右子節點高度的較大值 + 1 node.right_height = max(node.right_children.left_height, node.right_children.right_height) + 1 # 檢查是否仍有不平衡 if node.left_height - node.right_height >= 2: self.left_avertence(node) elif node.left_height - node.right_height <= -2: self.right_avertence(node) def right_avertence(self,node): # 右偏 就將當前節點的最左節點做父親 new_code = node() new_code.value = node.value new_code.left_children = node.left_children best_left = self.best_left_right(node.right_children) v = node.value # 返回的對象本身, if best_left == node.right_children and best_left.left_children == none: # 說明當前節點沒有有節點 node.value = best_left.value node.right_children = best_left.right_children else: node.value = best_left.left_children.value best_left.left_children = best_left.left_children.right_children node.left_children = new_code self.update_height(node) # 處理左偏情況 def left_avertence(self,node): new_code = node() new_code.value = node.value new_code.right_children = node.right_children best_right = self.best_left_right(node.left_children,1) v = node.value # 返回的對象本身, if best_right == node.left_children and best_right.right_children == none: # 說明當前節點沒有有節點 node.value = best_right.value node.left_children = best_right.left_children else: node.value = best_right.right_children.value best_right.right_children = best_right.right_children.left_children node.right_children = new_code self.update_height(node) # 返回node節點最左(右)子孫的父級 def best_left_right(self,node,type=0): # type=0 默認找最左子孫 if type == 0: if node.left_children == none: return node elif node.left_children.left_children == none: return node else: return self.best_left_right(node.left_children,type) else: if node.right_children == none: return node elif node.right_children.right_children == none: return node else: return self.best_left_right(node.right_children,type) # 前序(先中再左最后右) def front(self,node=none): if node == none: self.front_list = [] node = self.root # 輸出當前節點 self.front_list.append(node.value) # 先判斷左枝 if not node.left_children == none: self.front(node.left_children) # 再判斷右枝 if not node.right_children == none: self.front(node.right_children) # 返回最終結果 return self.front_list # 中序(先左再中最后右) def middle(self,node=none): if node == none: node = self.root # 先判斷左枝 if not node.left_children == none: self.middle(node.left_children) # 輸出當前節點 self.middle_list.append(node.value) # 再判斷右枝 if not node.right_children == none: self.middle(node.right_children) return self.middle_list # 后序(先左再右最后中) def after(self,node=none): if node == none: node = self.root # 先判斷左枝 if not node.left_children == none: self.after(node.left_children) # 再判斷右枝 if not node.right_children == none: self.after(node.right_children) self.after_list.append(node.value) return self.after_list # 節點刪除 def del_node(self,v,node=none): if node == none: node = self.root # 刪除根節點 if node.value == v: self.del_root(self.root) return # 刪除當前節點的左節點 if node.left_children: if node.left_children.value == v: self.del_left(node) return # 刪除當前節點的右節點 if node.right_children: if node.right_children.value == v: self.del_right(node) return if v > node.value: if node.right_children: self.del_node(v, node.right_children) else: print("刪除的元素不存在") else: if node.left_children: self.del_node(v, node.left_children) else: print("刪除的元素不存在") #刪除當前節點的右節點 def del_right(self,node): # 情況1 刪除節點沒有右枝 if node.right_children.right_children == none: node.right_children = node.right_children.left_children else: best_left = self.best_left_right(node.right_children.right_children) # 表示右枝最左孫就是右枝本身 if best_left == node.right_children.right_children and best_left.left_children == none: node.right_children.value = best_left.value node.right_children.right_children = best_left.right_children else: node.right_children.value = best_left.left_children.value best_left.left_children = best_left.left_children.right_children # 刪除當前節點的左節點 def del_left(self,node): # 情況1 刪除節點沒有右枝 if node.left_children.right_children == none: node.left_children = node.left_children.left_children else: best_left = self.best_left_right(node.left_children.right_children) # 表示右枝最左子孫就是右枝本身 if best_left == node.left_children.right_children and best_left.left_children == none: node.left_children.value = best_left.value node.left_children.right_children = best_left.right_children else: node.left_children.value = best_left.left_children.value best_left.left_children = best_left.left_children.right_children # 刪除根節點 def del_root(self,node): if node.right_children == none: if node.left_children == none: node.value = none else: self.root = node.left_children else: best_left = self.best_left_right(node.right_children) # 表示右枝最左子孫就是右枝本身 if best_left == node.right_children and best_left.left_children == none: node.value = best_left.value node.right_children = best_left.right_children else: node.value = best_left.left_children.value best_left.left_children = best_left.left_children.right_children # 搜索 def search(self,v,node=none): if node == none: node = self.root if node.value == v: return true if v > node.value: if not node.right_children == none: return self.search(v, node.right_children) else: if not node.left_children == none: return self.search(v, node.left_children) return falseif __name__ == '__main__': # 需要建立二叉樹的列表 list = [4, 6, 3, 1, 7, 9, 8, 5, 2] t = tree() t.create_tree(0,list) res = t.front() print('前序', res) |
執行結果:
前序 [4, 2, 1, 3, 7, 6, 5, 9, 8]
通過前序可以畫出二叉樹

完美,哈哈。
這是我鉆了兩天才寫出的代碼,哈哈,努力還是有回報的,加油。
下一步就是代碼優化了
以上就是本文的全部內容,希望對大家的學習有所幫助,也希望大家多多支持服務器之家。
原文鏈接:http://www.cnblogs.com/7749ha/p/9179086.html