前言
記得前段時間的文章么?redis使用位圖法記錄在線用戶的狀態,還是需要自己實現一個im在線用戶狀態的記錄,今天來講講另一方案,布隆過濾器
布隆過濾器的作用是加快判定一個元素是否在集合中出現的方法。因為其主要是過濾掉了大部分元素間的精確匹配,故稱為過濾器。
布隆過濾器
在日常生活工作,我們會經常遇到這的場景,從一個excel里面檢索一個信息在不在excel表中,還記得被ctrl+f支配的恐懼么,不扯了,軟件開發中,一般會使用散列表來實現,hash table也叫哈希表,哈希表的優點是快速準確,缺點是浪費儲存空間,我們這個場景,儲存登錄的userid到哈希表,當用戶規模十分巨大的時候,哈希表的儲存效率低的問題就顯示出來了,今天介紹一種數學工具:布隆過濾器,它只需要哈希表1/8到1/4的大小就能解決同樣的問題。
背書中
布隆過濾器(bloom filter)是由伯頓·布隆(burton bloom)于1970年提出來的,它實際上是一個很長的二進制向量和一系列隨機映射函數。
原理
使用我們這個場景,來講原理吧,假設我們的個人網站同時在線人數達到1億(意淫一下),要存儲這一億人的在線狀態,先構建一個16億比特位即兩億字節的向量,然后把這16億個比特位都記為0。對于每一個登錄用的userid,使用8個不同的算法產出8個不同信息指紋,在用一個算法把這8個信息隱身到這16億個比特位的8個位置上,把這8個位置都設置成1,這樣就構建成了一個記錄一億用戶在線狀態的布隆過濾器。
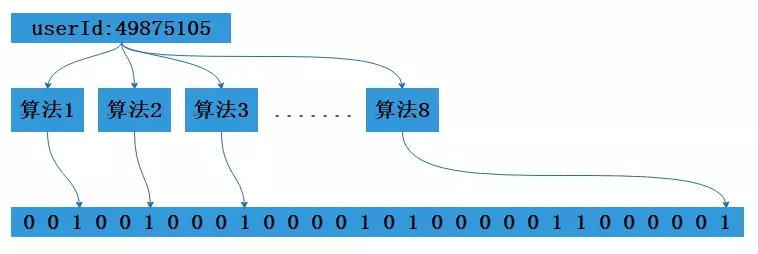
1億在線用戶的布隆過濾器
檢索就是同樣的原理,使用相同的算法對要檢索的userid產生8個信息指紋,然后在看這八個信息指紋在這16億比特位對應的值是否為1,都為1就說明這個userid在線,下面就用java代碼來實現一個布隆過濾器。
java實現布隆過濾器
先實現一個簡單的布隆過濾器
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
|
package edu.se;import java.util.bitset;/** * @author zhaoweinan * @date 2018/10/28 * @description */public class bloomfileter { //使用加法hash算法,所以定義了一個8個元素的質數數組 private static final int[] primes = new int[]{2, 3, 5, 7, 11, 13, 17, 19}; //用八個不同的質數,相當于構建8個不同算法 private hash[] hashlist = new hash[primes.length]; //創建一個長度為10億的比特位 private bitset bits = new bitset(256 << 22); public bloomfileter() { for (int i = 0; i < primes.length; i++) { //使用8個質數,創建八種算法 hashlist[i] = new hash(primes[i]); } } //添加元素 public void add(string value) { for (hash f : hashlist) { //算出8個信息指紋,對應到2的32次方個比特位上 bits.set(f.hash(value), true); } } //判斷是否在布隆過濾器中 public boolean contains(string value) { if (value == null) { return false; } boolean ret = true; for (hash f : hashlist) { //查看8個比特位上的值 ret = ret && bits.get(f.hash(value)); } return ret; } //加法hash算法 public static class hash { private int prime; public hash(int prime) { this.prime = prime; } public int hash(string key) { int hash, i; for (hash = key.length(), i = 0; i < key.length(); i++) { hash += key.charat(i); } return (hash % prime); } } public static void main(string[] args) { bloomfileter bloomfileter = new bloomfileter(); system.out.println(bloomfileter.contains("5324512515")); bloomfileter.add("5324512515"); //維護1億個在線用戶 for (int i = 1 ; i < 100000000 ; i ++){ bloomfileter.add(string.valueof(i)); } long begin = system.currenttimemillis(); system.out.println(begin); system.out.println(bloomfileter.contains("5324512515")); long end = system.currenttimemillis(); system.out.println(end); system.out.println("判斷5324512515是否在線使用了:" + (begin - end)); }} |
這段代碼是構建了一個10億位的bitset,然后把一億個userid加入到了我們的布隆過濾器中,最近判斷5324512515這個userid是否登錄,打出代碼的執行時間
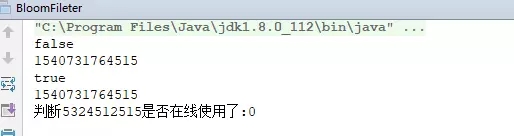
維護了1億個userid以后檢索5324512515是否登錄,代碼執行時間很短
在讓我們來看看內存占用的情況

jvm整個的內存情況
再來看看bloomfileter這個類的實例,就占用了100多mb

實例的大小
看來布隆過濾器對于儲存的效率確實很高
布隆過濾器的誤識別問題
布隆過濾器的好處在于快速、省空間,但是有一定的誤識別率,這個概率很小,要計算出現誤識別的概率并不難,下面貼一段書上的話
假定布隆過濾器有m比特,里面有n個元素,每個元素對應k個信息指紋的hash函數,在這個布隆過濾器插入一個元素,那么比特位被設置成1的概率為1/m,它依然為0的概率為1-1/m,那么k個哈希函數都沒有把他設置成1的概率為1-1/m的k次方,一個比特在插入了n個元素后,被設置為1的概率為1減1-1/m的kn次方,最后書上給出了一個公式,在這里就不貼了,就貼一個表吧,是m/n比值不同,以及k分別為不同的值得情況下的假陽性概率:
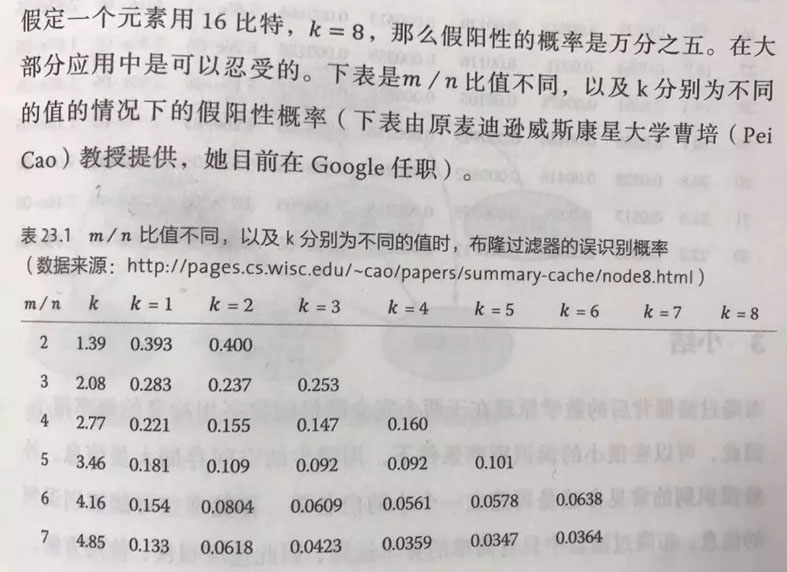
書上的表,直接拍下來的
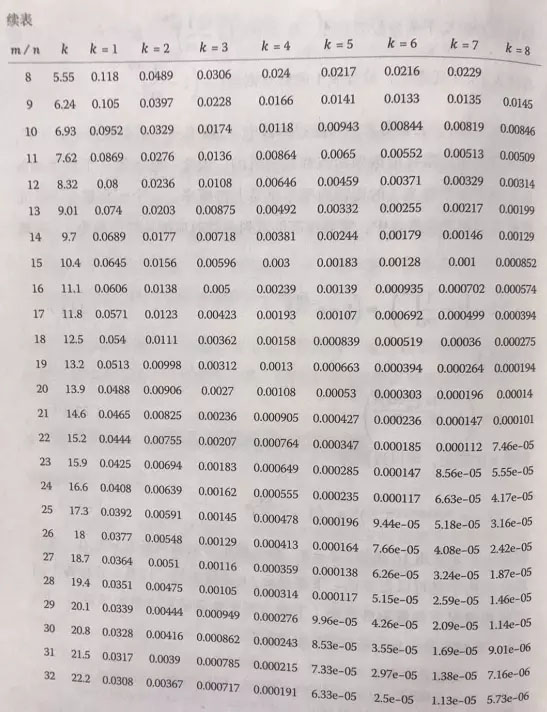
書上的表,直接拍下來的
布隆過濾器就為大家說到這里,歡迎大家來交流,指出文中一些說錯的地方,讓我加深認識。
總結
以上就是這篇文章的全部內容了,希望本文的內容對大家的學習或者工作具有一定的參考學習價值,如果有疑問大家可以留言交流,謝謝大家對服務器之家的支持。
原文鏈接:https://www.jianshu.com/p/7634eaea3e26