一、基本思想
希爾排序是把記錄按下標的一定增量分組,對每組使用直接插入排序算法排序;隨著增量逐漸減少,每組包含的關鍵詞越來越多,當增量減至1時,整個文件恰被分成一組,算法便終止。
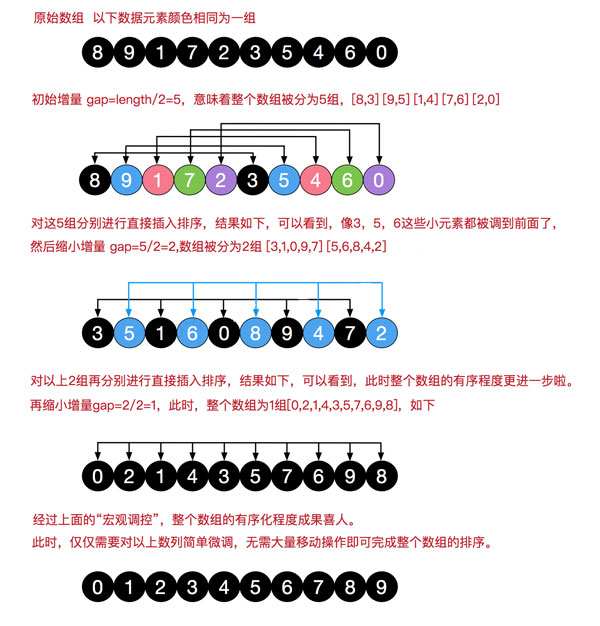
簡單插入排序很循規(guī)蹈矩,不管數(shù)組分布是怎么樣的,依然一步一步的對元素進行比較,移動,插入,比如[5,4,3,2,1,0]這種倒序序列,數(shù)組末端的0要回到首位置很是費勁,比較和移動元素均需n-1次。而希爾排序在數(shù)組中采用跳躍式分組的策略,通過某個增量將數(shù)組元素劃分為若干組,然后分組進行插入排序,隨后逐步縮小增量,繼續(xù)按組進行插入排序操作,直至增量為1。希爾排序通過這種策略使得整個數(shù)組在初始階段達到從宏觀上看基本有序,小的基本在前,大的基本在后。然后縮小增量,到增量為1時,其實多數(shù)情況下只需微調即可,不會涉及過多的數(shù)據(jù)移動。
我們來看下希爾排序的基本步驟,在此我們選擇增量gap=length/2,縮小增量繼續(xù)以gap = gap/2的方式,這種增量選擇我們可以用一個序列來表示,{n/2,(n/2)/2...1},稱為增量序列。希爾排序的增量序列的選擇與證明是個數(shù)學難題,我們選擇的這個增量序列是比較常用的,也是希爾建議的增量,稱為希爾增量,但其實這個增量序列不是最優(yōu)的。此處我們做示例使用希爾增量。
二、代碼實現(xiàn)
在希爾排序的理解時,我們傾向于對于每一個分組,逐組進行處理,但在代碼實現(xiàn)中,我們可以不用這么按部就班地處理完一組再調轉回來處理下一組(這樣還得加個for循環(huán)去處理分組)比如[5,4,3,2,1,0] ,首次增量設gap=length/2=3,則為3組[5,2] [4,1] [3,0],實現(xiàn)時不用循環(huán)按組處理,我們可以從第gap個元素開始,逐個跨組處理。同時,在插入數(shù)據(jù)時,可以采用元素交換法尋找最終位置,也可以采用數(shù)組元素移動法尋覓。希爾排序的代碼比較簡單,如下:
- package sortdemo;
- import java.util.Arrays;
- public class ShellSort {
- public static void main(String []args){
- int []arr ={1,4,2,7,9,8,3,6};
- sort(arr);
- System.out.println(Arrays.toString(arr));
- int []arr1 ={1,4,2,7,9,8,3,6};
- sort1(arr1);
- System.out.println(Arrays.toString(arr1));
- }
- /**
- * 希爾排序 針對有序序列在插入時采用交換法
- * @param arr
- */
- public static void sort(int []arr){
- //增量gap,并逐步縮小增量
- for(int gap=arr.length/2;gap>0;gap/=2){
- //從第gap個元素,逐個對其所在組進行直接插入排序操作
- for(int i=gap;i<arr.length;i++){
- int j = i;
- while(j-gap>=0 && arr[j]<arr[j-gap]){
- //插入排序采用交換法
- swap(arr,j,j-gap);
- j-=gap;
- }
- }
- }
- }
- /**
- * 希爾排序 針對有序序列在插入時采用移動法。
- * @param arr
- */
- public static void sort1(int []arr){
- //增量gap,并逐步縮小增量
- for(int gap=arr.length/2;gap>0;gap/=2){
- //從第gap個元素,逐個對其所在組進行直接插入排序操作
- for(int i=gap;i<arr.length;i++){
- int j = i;
- int temp = arr[j];
- if(arr[j]<arr[j-gap]){
- while(j-gap>=0 && temp<arr[j-gap]){
- //移動法
- arr[j] = arr[j-gap];
- j-=gap;
- }
- arr[j] = temp;
- }
- }
- }
- }
- /**
- * 交換數(shù)組元素
- * @param arr
- * @param a
- * @param b
- */
- public static void swap(int []arr,int a,int b){
- arr[a] = arr[a]+arr[b];
- arr[b] = arr[a]-arr[b];
- arr[a] = arr[a]-arr[b];
- }
- }
三、總結
本文介紹了希爾排序的基本思想及其代碼實現(xiàn),希爾排序中對于增量序列的選擇十分重要,直接影響到希爾排序的性能。我們上面選擇的增量序列{n/2,(n/2)/2...1}(希爾增量),其最壞時間復雜度依然為O(n2),一些經過優(yōu)化的增量序列如Hibbard經過復雜證明可使得最壞時間復雜度為O(n3/2)。希爾排序的介紹到此為止。
以上就是圖解排序算法之希爾排序Java實現(xiàn)的詳細內容,更多關于希爾排序 Java的資料請關注服務器之家其它相關文章!
原文鏈接:https://www.cnblogs.com/chengxiao/p/6104371.html