堆
堆(heap)是計算機科學中一類特殊的數據結構的統稱,通常是一個可以被看做一棵樹的數組對象。
堆{k1,k2,ki,…,kn} (ki <= k2i,ki <= k2i+1)|(ki >= k2i,ki >= k2i+1), (i = 1,2,3,4...n/2)
關于堆:
- 堆中某個節點的值總是不大于或不小于其父節點的值;
- 堆總是一棵完全二叉樹(下面)。
- 將根節點最大的堆叫做最大堆或大根堆,根節點最小的堆叫做最小堆或小根堆。
完全二叉樹
說到堆排序,就不能不提完全二叉樹,這些基本概念在網上到處都是,我摘了個最簡單的。。
完全二叉樹:除最后一層外,每一層上的節點數均達到最大值;在最后一層上只缺少右邊的若干結點。
我自己總結認為,正是因為有下面兩個特點,
- 只允許最后一層有空缺結點且空缺在右邊,即葉子結點只能在層次最大的兩層上出現(存儲方式的規則性);
- 若i>1,tree的雙親為tree[i div 2](其父子結點值的規律性);
才使得其進行排序非常方便。
堆排序
堆排序求升序用大頂堆,求降序用小頂堆。
本例用求降序的小頂堆來解析。
堆排序步驟如下:
1、我們將數據(49、38、65、97、76、13、27、50)建立一個數組$arr;
2、用數組$arr建立一個小頂堆(主要步驟,會在代碼注釋里解釋,下圖是用一個數組建立小頂堆的過程);
3、將堆的根(最小的元素)與最后一個葉子交換,并將堆長度減一,跳到第二步;
4、重復2-3步,直到堆中只有一個結點,排序完成。

堆排序的php實現
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
//因為是數組,下標從0開始,所以,下標為n根結點的左子結點為2n+1,右子結點為2n+2; //初始化值,建立初始堆$arr=array(49,38,65,97,76,13,27,50);$arrsize=count($arr);//將第一次排序抽出來,因為最后一次排序不需要再交換值了。buildheap($arr,$arrsize);for($i=$arrsize-1;$i>0;$i--){ swap($arr,$i,0); $arrsize--; buildheap($arr,$arrsize); }//用數組建立最小堆function buildheap(&$arr,$arrsize){ //計算出最開始的下標$index,如圖,為數字"97"所在位置,比較每一個子樹的父結點和子結點,將最小值存入父結點中 //從$index處對一個樹進行循環比較,形成最小堆 for($index=intval($arrsize/2)-1; $index>=0; $index--){ //如果有左節點,將其下標存進最小值$min if($index*2+1<$arrsize){ $min=$index*2+1; //如果有右子結點,比較左右結點的大小,如果右子結點更小,將其結點的下標記錄進最小值$min if($index*2+2<$arrsize){ if($arr[$index*2+2]<$arr[$min]){ $min=$index*2+2; } } //將子結點中較小的和父結點比較,若子結點較小,與父結點交換位置,同時更新較小 if($arr[$min]<$arr[$index]){ swap($arr,$min,$index); } } }}//此函數用來交換下數組$arr中下標為$one和$another的數據function swap(&$arr,$one,$another){ $tmp=$arr[$one]; $arr[$one]=$arr[$another]; $arr[$another]=$tmp;} |
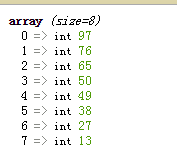
下面是排序的最終結果:
堆用來進行全排序,時間復雜度是o(nlogn)
而快排用來全排序,平均時間復雜度也是o(nlogn)
但堆排序可以用來求 topk 時,堆的時間復雜度為o(klog2(n),因為它只需要進行 k 輪排序即可。
以上就是本文的全部內容,希望對大家的學習有所幫助,也希望大家多多支持服務器之家。
原文鏈接:https://www.cnblogs.com/capacity-yang/p/13143875.html