一、堆排序算法原理和動態圖解
將待排序的序列構造成一個大頂堆。此時,整個序列的最大值就是堆頂的根節點。將它移走(其實就是將其與堆數組的末尾元素交換,此時末尾元素就是最大值),然后將剩余的n-1個序列重新構造成一個堆,這樣就會得到n個元素中的次最大值。如此反復執行,就能得到一個有序序列了。這個過程其實就是先構建一個最大/最小二叉堆,然后不停的取出最大/最小元素(頭結點),插入到新的隊列中,以此達到排序的目的。如下圖所示:
二、二叉樹定義
要了解堆首先得了解一下二叉樹,在計算機科學中,二叉樹是每個節點最多有兩個子樹的樹結構。通常子樹被稱作“左子樹”(left subtree)和“右子樹”(right subtree)。二叉樹常被用于實現二叉查找樹和二叉堆。二叉樹的每個結點至多只有二棵子樹(不存在度大于 2 的結點),二叉樹的子樹有左右之分,次序不能顛倒。二叉樹的第 i 層至多有 2i - 1 個結點;深度為 k 的二叉樹至多有 2k - 1 個結點;對任何一棵二叉樹 t,如果其終端結點數為 n0,度為 2 的結點數為 n2,則n0 = n2 + 1。二叉樹又分為完全二叉樹(complete binary tree)和滿二叉樹(full binary tree)。樹和二叉樹的三個主要差別:
- 樹的結點個數至少為 1,而二叉樹的結點個數可以為 0
- 樹中結點的最大度數沒有限制,而二叉樹結點的最大度數為 2
- 樹的結點無左、右之分,而二叉樹的結點有左、右之分
1.滿二叉樹:一棵深度為 k,且有 2k - 1 個節點稱之為滿二叉樹,即每一層上的節點數都是最大節點數。如下圖b所示:深度為3的滿二叉樹。
2.完全二叉樹:而在一棵二叉樹中,除最后一層外,若其余層都是滿的,并且最后一層或者是滿的,或者是在右邊缺少連續若干節點,則此二叉樹為完全二叉樹(complete binary tree)。如下圖a所示:是一個深度為4的完全二叉樹。
三、堆的定義
堆(二叉堆)可以視為一棵完全的二叉樹,完全二叉樹的一個“優秀”的性質是,除了最底層之外,每一層都是滿的,這使得堆可以利用數組來表示(普通的一般的二叉樹通常用鏈表作為基本容器表示),每一個結點對應數組中的一個元素。

對于7在數組存放的position=2,而它的子元素6的position=5=2*2[也就是父元素存放的位置]+1、子元素4的position=6=2*2[也就是父元素存放的位置]+2;同樣對于11在在數組存放的position=0,而它的子元素10的position=1=2*0[也就是父元素存放的位置]+1、子元素7的position=2=2*0[也就是父元素存放的位置]+2;所以對于i個元素,它的左右子節點在下標以0開始的數組中的位置分別為:2*i+1、2*i+2。那腦補一下,對于不完全二叉樹,如果用數組來存放會有什么問題呢?當然是中間有很多空的元素啦,所以說對于不完全二叉樹最好是用鏈表來存儲~。
堆的構建過程示例:建堆的核心內容是調整堆,使二叉樹滿足堆的定義(每個節點的值都不大于其父節點的值)。調堆的過程應該從最后一個非葉子節點開始,假設有數組a = {1, 3, 4, 5, 7, 2, 6, 8, 0}。那么調堆的過程如下圖,數組下標從0開始,a[3] = 5開始。分別與左孩子和右孩子比較大小,如果a[3]最大,則不用調整,否則和孩子中的值最大的一個交換位置,在圖1中是a[7] > a[3] > a[8],所以a[3]與a[7]對換,從圖1.1轉到圖1.2。

二叉堆(英語:binary heap)是一種特殊的堆,二叉堆是完全二叉樹或者是近似完全二叉樹。二叉堆滿足堆特性:父節點的鍵值總是保持固定的序關系于任何一個子節點的鍵值,且每個節點的左子樹和右子樹都是一個二叉堆。當父節點的鍵值總是大于或等于任何一個子節點的鍵值時為最大堆。 當父節點的鍵值總是小于或等于任何一個子節點的鍵值時為最小堆。二叉堆一般用數組來表示。如果根節點在數組中的位置是1,第n個位置的子節點分別在2n和 2n+1。因此,第1個位置的子節點在2和3,第2個位置的子節點在4和5。以此類推。這種基于1的數組存儲方式便于尋找父節點和子節點。如果存儲數組的下標基于0,那么下標為i的節點的子節點是2i + 1與2i + 2;其父節點的下標是⌊floor((i − 1) ∕ 2)⌋。函數floor(x)的功能是“向下取整”,或者說“向下舍入”,即取不大于x的最大整數(與“四舍五入”不同,向下取整是直接取按照數軸上最接近要求值的左邊值,即不大于要求值的最大的那個值)。比如floor(1.1)、floor(1.9)都返回1。對于堆定義中的堆結構插入元素:對于二叉堆來說,要插入一個新元素其整個過程是怎么樣的呢?這里還是以我們之前的那個二叉堆進行說明,以插入"9"為例:

目前肯定不滿足二叉堆的要求,父接點6是小于新插入的節點9的,所以兩者進行位置交換:
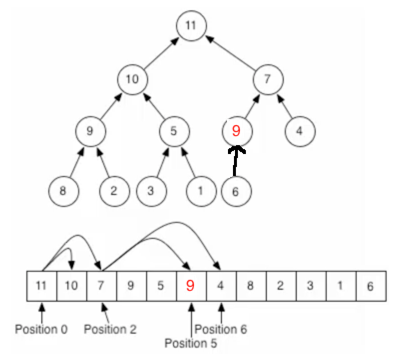
同樣的思路,父節點7比子節點9要小,所以需要調換位置:
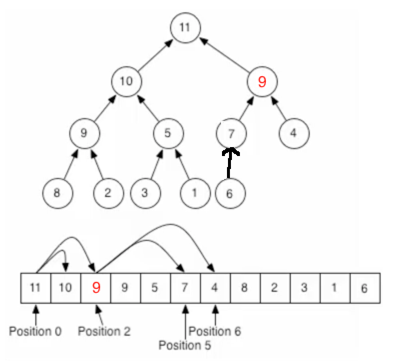
至此元素插入完成,也符合二叉堆父元素大于子元素的規則,從添加過程中可以發現:只需更改待比較的元素,其它的任何元素位置不需要動,所以效率還是很高的。對于堆定義中的堆結構刪除元素:這里以刪除根結點為例【因為刪除根節點是最重要的,所以以它為例】,整個過程如下:

這時當然是不符合二叉堆的規則,接著這樣來做:

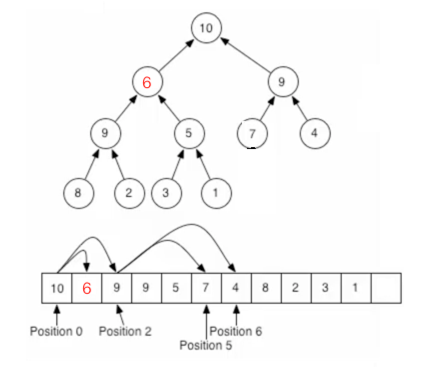
同理繼續進行處理:

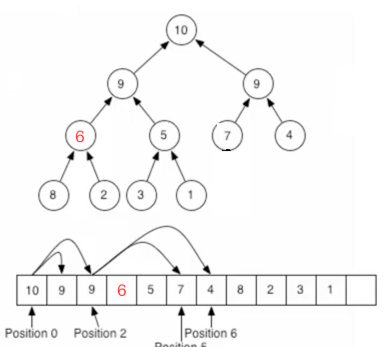
繼續:

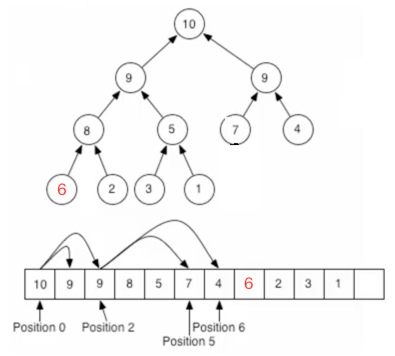
經過這些動作之后就將一個根結點給刪除掉了,可以發現其實跟插入一個元素一樣,只需更改待比較的元素,其它的任何元素位置不需要動,那像這種每次移除掉最大的值有啥用呢?堆排序就產生了,因為每次從根節點拿肯定是最大的數【以最大堆來說】,這樣拿出來的數就成了一個有序的數列了。注意:對于一個很大的堆,這種存儲是低效的。因為節點的子節點很可能在另外一個內存頁中。b-heap是一種效率更高的存儲方式,把每個子樹放到同一內存頁。如果用指針鏈表存儲堆,那么需要能訪問葉節點的方法。可以對二叉樹“穿線”(threading)方式,來依序遍歷這些節點。
四、堆排序java代碼實現
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
|
package com.luna.sort;public class heapsortmaxandmin{ public static void main(string[] args) { int[] array = { 19, 38, 7, 36, 5, 5, 3, 2, 1, 0, 56 }; system.out.println("排序前:"); for (int i = 0; i < array.length; i++) { system.out.print(array[i] + ","); } system.out.println(); system.out.println("分割線---------------"); heapsort(array); system.out.println("排序后:"); for (int i = 0; i < array.length; i++) { system.out.print(array[i] + ","); } } public static void heapsort(int[] array) { if (array == null || array.length == 1) return; buildarraytoheap(array); //將數組元素轉化為大頂堆/小頂堆 for (int i = array.length - 1; i >= 1; i--) { // 經過上面的一些列操作,目前array[0]是當前數組里最大的元素,需要和末尾的元素交換,然后拿出最大的元素 swap(array, 0, i); /** * 交換完后,下次遍歷的時候,就應該跳過最后一個元素,也就是最大的那個 * 值,然后開始重新構建最大堆堆的大小就減去1,然后從0的位置開始最大堆 */// buildmaxheap(array, i, 0); buildminheap(array, i, 0); } } // 構建堆 public static void buildarraytoheap(int[] array) { if (array == null || array.length == 1) return; //遞推公式就是 int root = 2*i, int left = 2*i+1, int right = 2*i+2; int cursor = array.length / 2; for (int i = cursor; i >= 0; i--) { // 這樣for循環下,就可以第一次排序完成// buildmaxheap(array, array.length, i); buildminheap(array, array.length, i); } } //大頂堆 public static void buildmaxheap(int[] array, int heapsieze, int index) { int left = index * 2 + 1; // 左子節點 int right = index * 2 + 2; // 右子節點 int maxvalue = index; // 暫時定在index的位置就是最大值 // 如果左子節點的值,比當前最大的值大,就把最大值的位置換成左子節點的位置 if (left < heapsieze && array[left] > array[maxvalue]) { maxvalue = left; } // 如果右子節點的值,比當前最大的值大,就把最大值的位置換成右子節點的位置 if (right < heapsieze && array[right] > array[maxvalue]) { maxvalue = right; } // 如果不相等說明,這個子節點的值有比自己大的,位置發生了交換了位置 if (maxvalue != index) { swap(array, index, maxvalue); // 就要交換位置元素 // 交換完位置后還需要判斷子節點是否打破了最大堆的性質。最大堆性質:兩個子節點都比父節點小。 buildmaxheap(array, heapsieze, maxvalue); } } //小頂堆 public static void buildminheap(int[] array, int heapsieze, int index) { int left = index * 2 + 1; // 左子節點 int right = index * 2 + 2; // 右子節點 int maxvalue = index; // 暫時定在index的位置就是最小值 // 如果左子節點的值,比當前最小的值小,就把最小值的位置換成左子節點的位置 if (left < heapsieze && array[left] < array[maxvalue]) { maxvalue = left; } // 如果右子節點的值,比當前最小的值小,就把最小值的位置換成左子節點的位置 if (right < heapsieze && array[right] < array[maxvalue]) { maxvalue = right; } // 如果不相等說明這個子節點的值有比自己小的,位置發生了交換了位置 if (maxvalue != index) { swap(array, index, maxvalue); // 就要交換位置元素 // 交換完位置后還需要判斷子節點是否打破了最小堆的性質。最小性質:兩個子節點都比父節點大。 buildminheap(array, heapsieze, maxvalue); } } // 數組元素交換 public static void swap(int[] a, int i, int j) { int temp = a[i]; a[i] = a[j]; a[j] = temp; }} |
大頂堆優化實現算法:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
|
import java.util.arrays;public class maxheapsort { private int[] arr; public maxheapsort(int[] arr){ this.arr = arr; } /** * 堆排序的主要入口方法,共兩步。 */ public void sort(){ /* * 第一步:將數組堆化 * beginindex = 第一個非葉子節點。 * 從第一個非葉子節點開始即可。無需從最后一個葉子節點開始。 * 葉子節點可以看作已符合堆要求的節點,根節點就是它自己且自己以下值為最大。 */ int len = arr.length - 1; int beginindex = (len - 1) >> 1; for(int i = beginindex; i >= 0; i--){ maxheapify(i, len); } /* * 第二步:對堆化數據排序 * 每次都是移出最頂層的根節點a[0],與最尾部節點位置調換,同時遍歷長度 - 1。 * 然后從新整理被換到根節點的末尾元素,使其符合堆的特性。 * 直至未排序的堆長度為 0。 */ for(int i = len; i > 0; i--){ swap(0, i); maxheapify(0, i - 1); } } private void swap(int i,int j){ int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } /** * 調整索引為 index 處的數據,使其符合堆的特性。 * @param index 需要堆化處理的數據的索引 * @param len 未排序的堆(數組)的長度 */ private void maxheapify(int index,int len){ int li = (index << 1) + 1; // 左子節點索引 int ri = li + 1; // 右子節點索引 int cmax = li; // 子節點值最大索引,默認左子節點。 if(li > len) return; // 左子節點索引超出計算范圍,直接返回。 if(ri <= len && arr[ri] > arr[li]) // 先判斷左右子節點,哪個較大。 cmax = ri; if(arr[cmax] > arr[index]){ swap(cmax, index); // 如果父節點被子節點調換, maxheapify(cmax, len); // 則需要繼續判斷換下后的父節點是否符合堆的特性。 } } /** * 測試用例 * 輸出: * [0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6, 7, 7, 7, 8, 8, 8, 9, 9, 9] */ public static void main(string[] args) { int[] arr = new int[]{3,5,3,0,8,6,1,5,8,6,2,4,9,4,7,0,1,8,9,7,3,1,2,5,9,7,4,0,2,6}; new maxheapsort(arr).sort(); system.out.println(arrays.tostring(arr)); }} |
總結
本篇文章就到這里了,希望能給你帶來幫助,也希望您能夠多多關注服務器之家的更多內容!
原文鏈接:https://blog.csdn.net/u011635492/article/details/83046477