pandas批量處理體測成績

import numpy as np
import pandas as pd
from pandas import Series,DataFrame
import matplotlib.pyplot as plt
data = pd.read_excel("/Users/zhucan/Desktop/18級高一體測成績匯總.xls")

cond = data["班級"] != "班級"
data = data[cond]

data.fillna(0,inplace=True)
data.isnull().any()   #沒有空數(shù)據(jù)了

結(jié)果：

班級       False

性別       False

姓名       False

1000米    False

50米      False

跳遠(yuǎn)       False

體前屈      False

引體       False

肺活量      False

身高       False

體重       False

dtype: bool

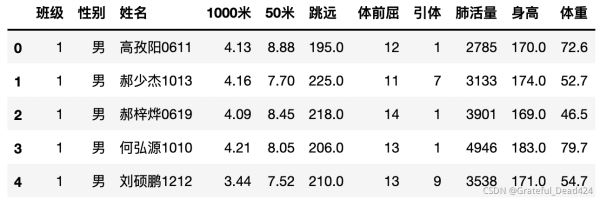
data.head()

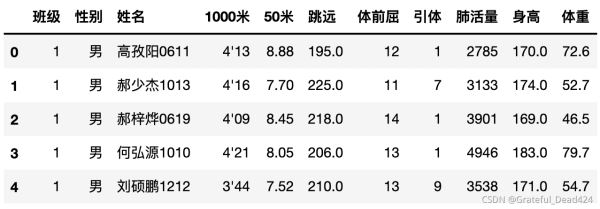
#1000米成績有string 有int
def convert(x):
  if isinstance(x,str):
      minute,second = x.split("'")
      int(minute)
      minute = int(minute)
      second = int(second)
      return minute + second/100.0
  else:
      return x
data["1000米"] = data["1000米"].map(convert)

score = pd.read_excel("/Users/zhucan/Desktop/體側(cè)成績評分表.xls",header=[0,1])
score

def convert(item):
  m,s = item.strip('"').split("'")
  m,s =int(m),int(s)
  return m+s/100.0
score.iloc[:,-4] = score.iloc[:,-4].map(convert) 
def convert(item):
  m,s = item.strip('"').split("'")
  m,s =int(m),int(s)
  return m+s/100.0    
score.iloc[:,-2] = score.iloc[:,-2].map(convert)
score

data.columns = ['班級', '性別', '姓名', '男1000', '男50米跑', '跳遠(yuǎn)', '體前屈', '引體', '肺活量', '身高', '體重']

data["男50米跑"] = data["男50米跑"].astype(np.float)
for col in ["男1000","男50米跑"]:
  #獲取成績的標(biāo)準(zhǔn)
  s = score[col]
  def convert(x):
      for i in range(len(s)):
          if x<=s["成績"].iloc[0]:
              if x == 0:
                  return 0 #沒有參加這個(gè)項(xiàng)目
              return 100
          elif x>s["成績"].iloc[-1]:
              return 0  #跑的太慢
          elif (x>s["成績"].iloc[i-1]) and (x<=s["成績"].iloc[i]):
              return s["分?jǐn)?shù)"].iloc[i]
  data[col + "成績"] = data[col].map(convert)

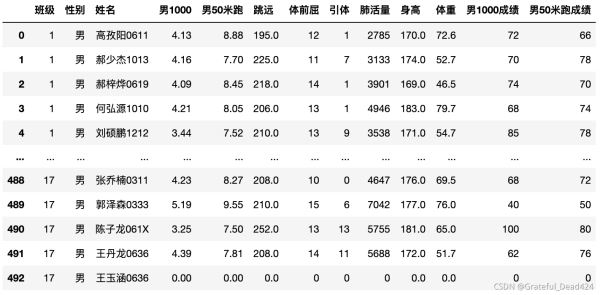
for col in ['跳遠(yuǎn)', '體前屈', '引體', '肺活量']:
  s = score["男"+col]
  def convert(x):
      for i in range(len(s)):
          if x>s["成績"].iloc[i]:
              return s["分?jǐn)?shù)"].iloc[i]
      return 0
  data[col+"成績"] = data[col].map(convert)

data.columns

 結(jié)果：

Index(['班級', '性別', '姓名', '男1000', '男50米跑', '跳遠(yuǎn)', '體前屈', '引體', '肺活量', '身高',
     '體重', '男1000成績', '男50米跑成績', '跳遠(yuǎn)成績', '體前屈成績', '引體成績', '肺活量成績'],
    dtype='object')

#根據(jù)索引的順序，去data取值
cols = ['班級', '性別', '姓名', '男1000','男1000成績','男50米跑','男50米跑成績','跳遠(yuǎn)','跳遠(yuǎn)成績','體前屈','體前屈成績','引體','引體成績', '肺活量','肺活量成績','身高','體重']
data[cols]

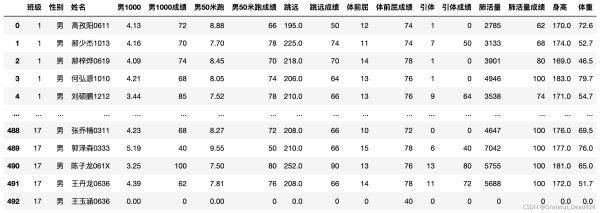
#計(jì)算BMI
data["BMI"] = data["體重"]/data["身高"]
def convert(x):
  if x>100:
      return x/100
  else:
      return x
data["身高"] = data["身高"].map(convert)
data["BMI"] = data["體重"]/(data["身高"])**2

def convert_bmi(x):
  if x >= 26.4:
      return 60
  elif (x <= 16.4) or (x > 23.3 and x <= 26.3):
      return 80
  elif x >= 16.5 and x <= 23.2:
      return 100
  else:
      return 0
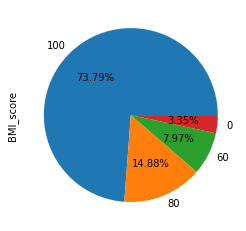
data["BMI_score"] = data["BMI"].map(convert_bmi)

#統(tǒng)計(jì)分析
data["BMI_score"].value_counts().plot(kind = "pie",autopct = "%0.2f%%")
#統(tǒng)計(jì)分析
data["BMI_score"].value_counts().plot(kind = "bar")

data.groupby(["男1000成績"])["BMI_score"].count().plot(kind = "bar")

 

adaboost

 值

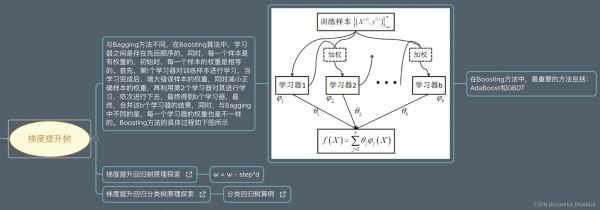
越大，特征越明顯，越被容易分開；越后面的學(xué)習(xí)器，權(quán)重越大

梯度提升樹沒有修改原來的數(shù)據(jù)，使用的是殘差，最終結(jié)果就是最后一棵樹

上面的圖不是GBDT

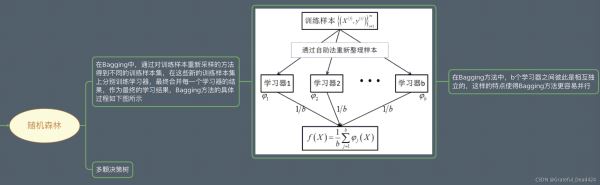
Boosting與Bagging模型相比，Boosting可以同時(shí)降低偏差和方差，Bagging只能降低模型的方差。在實(shí)際應(yīng)用中，Boosting算法也還是存在明顯的高方差問題，也就是過擬合。 

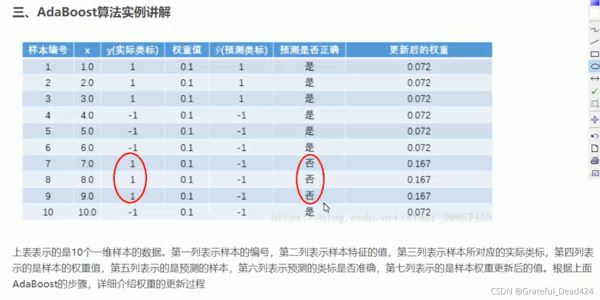
import numpy as np
y = np.array([0,1]*5)
y_ = np.array([0,0,0,0,0,0,0,1,0,1])
w = 0.1*(y != y_).sum()
round(w,1)

結(jié)果：

0.3

0.5*np.log((1-0.3)/0.3)
round((0.5*np.log((1-0.3)/0.3)),2)

 結(jié)果：

0.42

 

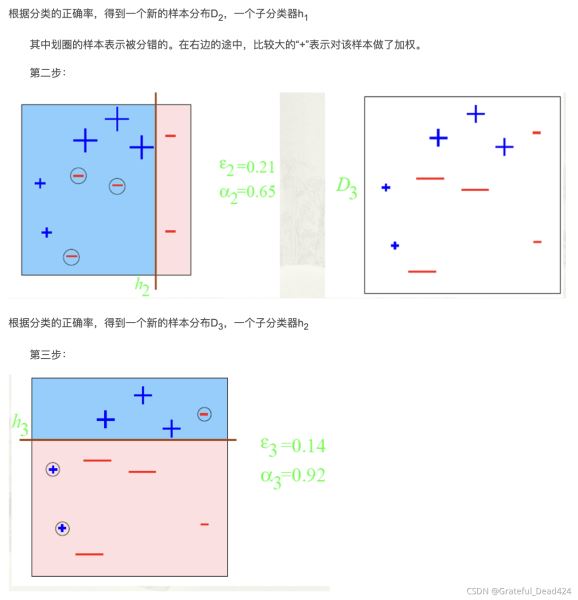
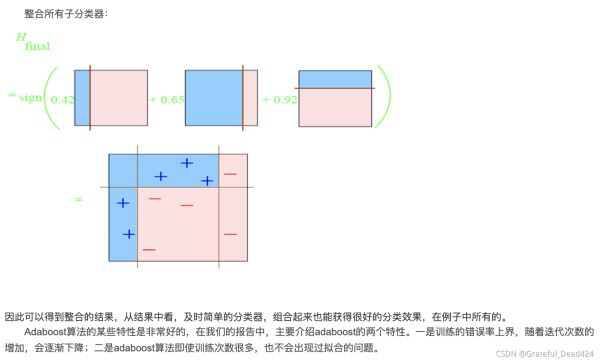
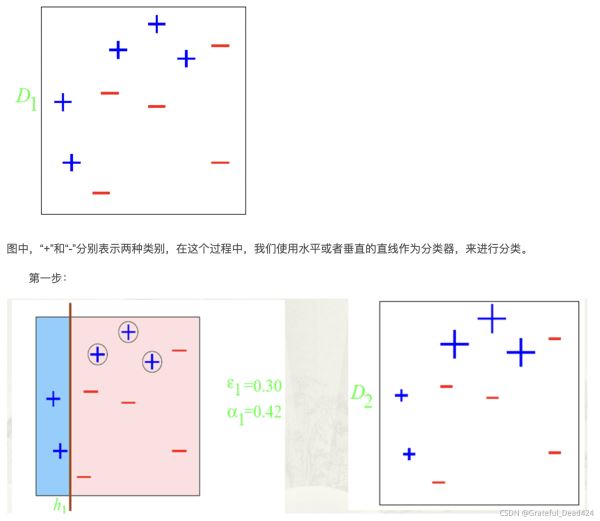
adaboost原理案例舉例

from sklearn.ensemble import AdaBoostClassifier
from sklearn import tree
import matplotlib.pyplot as plt
X = np.arange(10).reshape(-1,1)
y = np.array([1,1,1,-1,-1,-1,1,1,1,-1])
ada = AdaBoostClassifier(n_estimators=3)
ada.fit(X,y)

plt.figure(figsize = (9,6))
_ = tree.plot_tree(ada[0])

y_ = ada[0].predict(X),4
y_

結(jié)果：

array([ 1,  1,  1, -1, -1, -1, -1, -1, -1, -1])

#誤差率
e1 = np.round(0.1*(y != y_).sum(),4)
e1

結(jié)果：

0.3

#計(jì)算第一棵樹權(quán)重
#隨機(jī)森林中每棵樹的權(quán)重是一樣的
#adaboost提升樹中每棵樹的權(quán)重不同
a1 = np.round(1/2*np.log((1-e1)/e1),4)
a1

結(jié)果：

0.4236

#樣本預(yù)測準(zhǔn)確：更新的權(quán)重
w2 = 0.1*np.e**(-a1*y*y_)
w2 = w2/w2.sum()
np.round(w2,4)

結(jié)果：

array([0.0714, 0.0714, 0.0714, 0.0714, 0.0714, 0.0714, 0.1667, 0.1667,
     0.1667, 0.0714])

#樣本預(yù)測準(zhǔn)確：更新的權(quán)重
w2 = 0.1*np.e**(-a1*y*y_)
w2 = w2/w2.sum()
np.round(w2,4)

結(jié)果：

array([0.0714, 0.0714, 0.0714, 0.0714, 0.0714, 0.0714, 0.1667, 0.1667,
     0.1667, 0.0714])

從上述第一輪的整個(gè)迭代過程可以看出：被誤分類樣本的權(quán)值之和影響誤差率，誤差率影響基本分類器在最終分類器中所占的權(quán)重

分類函數(shù) f1(x)= a1*G1(x)= 0.4236G1(x)

plt.figure(figsize = (9,6))
_ = tree.plot_tree(ada[1])

e2 = 0.0714*3
e2

結(jié)果：

0.2142

a2 = np.round(1/2*np.log((1-e2)/e2),4)
a2

 結(jié)果：

0.6499

y_ = ada[1].predict(X)
#樣本預(yù)測準(zhǔn)確：更新的權(quán)重
w3 = w2*np.e**(-a2*y*y_)
w3 = w3/w3.sum()
np.round(w3,4)

結(jié)果：

array([0.0454, 0.0454, 0.0454, 0.1667, 0.1667, 0.1667, 0.106 , 0.106 ,
     0.106 , 0.0454])

plt.figure(figsize = (9,6))
_ = tree.plot_tree(ada[2])

樹劃分按照gini系數(shù);結(jié)果和按照誤差率是一致的～ 

y_ = ada[2].predict(X)
e3 = (w3*(y_ != y)).sum()
a3 = 1/2*np.log((1-e3)/e3)
a3
#樣本預(yù)測準(zhǔn)確：更新的權(quán)重
w4 = w3*np.e**(-a3*y*y_)
w4 = w4/w4.sum()
np.round(w4,4)

結(jié)果：

array([0.125 , 0.125 , 0.125 , 0.1019, 0.1019, 0.1019, 0.0648, 0.0648,
     0.0648, 0.125 ])

display(a1,a2,a3)

 結(jié)果：

0.4236

0.6498960745553556

0.7521752700597043

弱分類器合并成強(qiáng)分類器

綜上，將上面計(jì)算得到的a1、a2、a3各值代入G(x)中

G(x) = sign[f3(x)] = sign[ a1 * G1(x) + a2 * G2(x) + a3 * G3(x) ]

得到最終的分類器為：

G(x) = sign[f3(x)] = sign[ 0.4236G1(x) + 0.6496G2(x)+0.7514G3(x) ]

ada.predict(X)

結(jié)果：

array([ 1,  1,  1, -1, -1, -1,  1,  1,  1, -1])

y_predict = a1*ada[0].predict(X) +  a2*ada[1].predict(X) +a3*ada[2].predict(X)
y_predict
np.sign(y_predict).astype(np.int)

array([ 1,  1,  1, -1, -1, -1,  1,  1,  1, -1])

以上就是python機(jī)器學(xué)習(xí)Sklearn實(shí)戰(zhàn)adaboost算法示例詳解的詳細(xì)內(nèi)容，更多關(guān)于機(jī)器學(xué)習(xí)Sklearn實(shí)戰(zhàn)adaboost算法的資料請關(guān)注服務(wù)器之家其它相關(guān)文章！

原文鏈接：https://blog.csdn.net/Grateful_Dead424/article/details/121064899