前言:Java8之后新增挺多新東西,在網上找了些相關資料,關于HashMap在自己被血虐之后痛定思痛決定整理一下相關知識方便自己看。
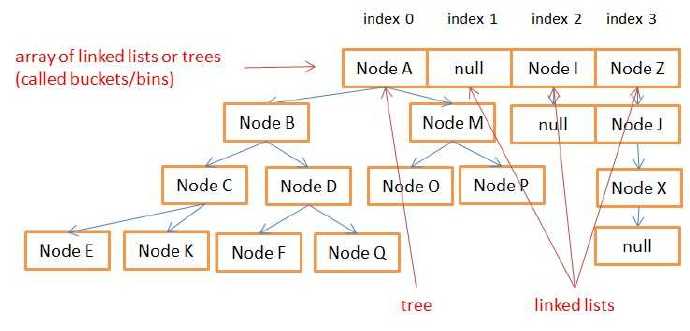
HashMap的存儲結構如圖:一個桶(bucket)上的節點多于8個則存儲結構是紅黑樹,小于8個是單向鏈表。
1:HashMap的一些屬性
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
public class HashMap<k,v> extends AbstractMap<k,v> implements Map<k,v>, Cloneable, Serializable {private static final long serialVersionUID = 362498820763181265L;// 默認的初始容量是16static final int DEFAULT_INITIAL_CAPACITY = 1 << 4;// 最大容量static final int MAXIMUM_CAPACITY = 1 << 30;// 默認的填充因子(以前的版本也有叫加載因子的)static final float DEFAULT_LOAD_FACTOR = 0.75f;// 這是一個閾值,當桶(bucket)上的鏈表數大于這個值時會轉成紅黑樹,put方法的代碼里有用到static final int TREEIFY_THRESHOLD = 8;// 也是閾值同上一個相反,當桶(bucket)上的鏈表數小于這個值時樹轉鏈表static final int UNTREEIFY_THRESHOLD = 6;// 看源碼注釋里說是:樹的最小的容量,至少是 4 x TREEIFY_THRESHOLD = 32 然后為了避免(resizing 和 treeification thresholds) 設置成64static final int MIN_TREEIFY_CAPACITY = 64;// 存儲元素的數組,總是2的倍數transient Node<k,v>[] table;transient Set<map.entry<k,v>> entrySet;// 存放元素的個數,注意這個不等于數組的長度。transient int size;// 每次擴容和更改map結構的計數器transient int modCount;// 臨界值 當實際大小(容量*填充因子)超過臨界值時,會進行擴容int threshold;// 填充因子final float loadFactor; |
2:HashMap的構造方法
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
// 指定初始容量和填充因子的構造方法public HashMap(int initialCapacity, float loadFactor) {// 指定的初始容量非負if (initialCapacity < 0)throw new IllegalArgumentException(Illegal initial capacity: +initialCapacity);// 如果指定的初始容量大于最大容量,置為最大容量if (initialCapacity > MAXIMUM_CAPACITY)initialCapacity = MAXIMUM_CAPACITY;// 填充比為正if (loadFactor <= 0 || Float.isNaN(loadFactor))throw new IllegalArgumentException(Illegal load factor: +loadFactor);this.loadFactor = loadFactor;// 指定容量后,tableSizeFor方法計算出臨界值,put數據的時候如果超出該值就會擴容,該值肯定也是2的倍數// 指定的初始容量沒有保存下來,只用來生成了一個臨界值this.threshold = tableSizeFor(initialCapacity);}// 該方法保證總是返回大于cap并且是2的倍數的值,比如傳入999 返回1024static final int tableSizeFor(int cap) {int n = cap - 1;// 向右做無符號位移n |= n >>> 1;n |= n >>> 2;n |= n >>> 4;n |= n >>> 8;n |= n >>> 16;// 三目運算符的嵌套return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;}//構造函數2public HashMap(int initialCapacity) {this(initialCapacity, DEFAULT_LOAD_FACTOR);}//構造函數3public HashMap() {this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted} |
3:get和put的時候確定元素在數組中的位置
|
1
2
3
4
|
static final int hash(Object key) {int h;return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);} |
要確定位置
第一步:首先是要計算key的hash碼,是一個int類型數字。那后面的 h >>> 16 源碼注釋的說法是:為了避免hash碰撞(hash collisons)將高位分散到低位上了,這是綜合考慮了速度,性能等各方面因素之后做出的。
第二步: h是hash碼,length是上面Node[]數組的長度,做與運算 h & (length-1)。由于length是2的倍數-1后它的二進制碼都是1而1與上其他數的結果可能是0也可能是1,這樣保證運算后的均勻性。也就是hash方法保證了結果的均勻性,這點非常重要,會極大的影響HashMap的put和get性能。看下圖對比:

圖3.1是非對稱的hash結果
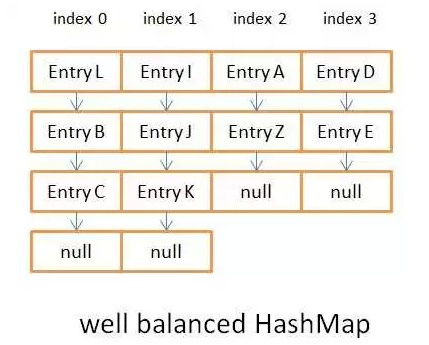
圖3.2是均衡的hash結果
這兩個圖的數據不是很多,如果鏈表長度超過8個會轉成紅黑樹。那個時候看著會更明顯,jdk8之前一直是鏈表,鏈表查詢的復雜度是O(n)而紅黑樹由于其自身的特點,查詢的復雜度是O(log(n))。如果hash的結果不均勻會極大影響操作的復雜度。相關的知識這里有一個<a href=”http://blog.chinaunix.net/uid-26575352-id-3061918.html”>紅黑樹基礎知識博客 </a>網上還有個例子來驗證:自定義了一個對象來做key,調整hashCode()方法來看put值得時間
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
public class MutableKeyTest {public static void main(String args[]){class MyKey {Integer i;public void setI(Integer i) {this.i = i;}public MyKey(Integer i) {this.i = i;}@Overridepublic int hashCode() {// 如果返回1// return 1return i;}// object作為key存map里,必須實現equals方法@Overridepublic boolean equals(Object obj) {if (obj instanceof MyKey) {return i.equals(((MyKey)obj).i);} else {return false;}}}// 我機器配置不高,25000的話正常情況27毫秒,可以用2500萬試試,如果hashCode()方法返回1的話,250萬就卡死Map<MyKey,String> map = new HashMap<>(25000,1);Date begin = new Date();for (int i = 0; i < 20000; i++){map.put(new MyKey(i), "test " + i);}Date end = new Date();System.out.println("時間(ms) " + (end.getTime() - begin.getTime())); |
4:get方法
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
public V get(Object key) {Node<k,v> e;return (e = getNode(hash(key), key)) == null ? null : e.value;}final Node<k,v> getNode(int hash, Object key) {Node<k,v>[] tab; Node<k,v> first, e; int n; K k;// hash & (length-1)得到紅黑樹的樹根位置或者是鏈表的表頭if ((tab = table) != null && (n = tab.length) > 0 &&(first = tab[(n - 1) & hash]) != null) {if (first.hash == hash && // always check first node((k = first.key) == key || (key != null && key.equals(k))))return first;if ((e = first.next) != null) {// 如果是樹,遍歷紅黑樹復雜度是O(log(n)),得到節點值if (first instanceof TreeNode)return ((TreeNode<k,v>)first).getTreeNode(hash, key);// else是鏈表結構do {if (e.hash == hash &&((k = e.key) == key || (key != null && key.equals(k))))return e;} while ((e = e.next) != null);}}return null;} |
5 :put方法,put的時候根據 h & (length – 1) 定位到那個桶然后看是紅黑樹還是鏈表再putVal
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
public V put(K key, V value) {return putVal(hash(key), key, value, false, true);}final V putVal(int hash, K key, V value, boolean onlyIfAbsent,boolean evict) {Node<k,v>[] tab; Node<k,v> p; int n, i;// 如果tab為空或長度為0,則分配內存resize()if ((tab = table) == null || (n = tab.length) == 0)n = (tab = resize()).length;// (n - 1) & hash找到put位置,如果為空,則直接putif ((p = tab[i = (n - 1) & hash]) == null)tab[i] = newNode(hash, key, value, null);else {Node<k,v> e; K k;// 第一節節點hash值同,且key值與插入key相同if (p.hash == hash &&((k = p.key) == key || (key != null && key.equals(k))))e = p;else if (p instanceof TreeNode)// 紅黑樹的put方法比較復雜,putVal之后還要遍歷整個樹,必要的時候修改值來保證紅黑樹的特點e = ((TreeNode<k,v>)p).putTreeVal(this, tab, hash, key, value);else {// 鏈表for (int binCount = 0; ; ++binCount) {if ((e = p.next) == null) {// e為空,表示已到表尾也沒有找到key值相同節點,則新建節點p.next = newNode(hash, key, value, null);// 新增節點后如果節點個數到達閾值,則將鏈表轉換為紅黑樹if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1sttreeifyBin(tab, hash);break;}// 容許空key空valueif (e.hash == hash &&((k = e.key) == key || (key != null && key.equals(k))))break;p = e;}}// 更新hash值和key值均相同的節點Value值if (e != null) { // existing mapping for keyV oldValue = e.value;if (!onlyIfAbsent || oldValue == null)e.value = value;afterNodeAccess(e);return oldValue;}}++modCount;if (++size > threshold)resize();afterNodeInsertion(evict);return null;} |
6:resize方法
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
|
final Node<K,V>[] resize() {Node<K,V>[] oldTab = table;int oldCap = (oldTab == null) ? 0 : oldTab.length;int oldThr = threshold;int newCap, newThr = 0;if (oldCap > 0) {if (oldCap >= MAXIMUM_CAPACITY) {threshold = Integer.MAX_VALUE;return oldTab;}// 這一句比較重要,可以看出每次擴容是2倍else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&oldCap >= DEFAULT_INITIAL_CAPACITY)newThr = oldThr << 1; // double threshold}else if (oldThr > 0) // initial capacity was placed in thresholdnewCap = oldThr;else { // zero initial threshold signifies using defaultsnewCap = DEFAULT_INITIAL_CAPACITY;newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);}if (newThr == 0) {float ft = (float)newCap * loadFactor;newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?(int)ft : Integer.MAX_VALUE);}threshold = newThr;@SuppressWarnings({"rawtypes","unchecked"})Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];table = newTab;if (oldTab != null) {for (int j = 0; j < oldCap; ++j) {Node<K,V> e;if ((e = oldTab[j]) != null) {oldTab[j] = null;if (e.next == null)newTab[e.hash & (newCap - 1)] = e;else if (e instanceof TreeNode)((TreeNode<K,V>)e).split(this, newTab, j, oldCap);else { // preserve orderNode<K,V> loHead = null, loTail = null;Node<K,V> hiHead = null, hiTail = null;Node<K,V> next;do {next = e.next;if ((e.hash & oldCap) == 0) {if (loTail == null)loHead = e;elseloTail.next = e;loTail = e;}else {if (hiTail == null)hiHead = e;elsehiTail.next = e;hiTail = e;}} while ((e = next) != null);if (loTail != null) {loTail.next = null;newTab[j] = loHead;}if (hiTail != null) {hiTail.next = null;newTab[j + oldCap] = hiHead;}}}}}return newTab;} |
以上所述是小編給大家介紹的Java8 HashMap的實現原理分析的相關知識,希望對大家有所幫助!