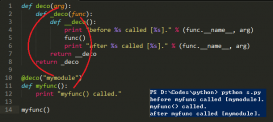
在PyTorch中可以方便的驗證SoftMax交叉熵損失和對輸入梯度的計算
關于softmax_cross_entropy求導的過程,可以參考HERE
示例:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
# -*- coding: utf-8 -*-import torchimport torch.autograd as autogradfrom torch.autograd import Variableimport torch.nn.functional as Fimport torch.nn as nnimport numpy as np# 對data求梯度, 用于反向傳播data = Variable(torch.FloatTensor([[1.0, 2.0, 3.0], [1.0, 2.0, 3.0], [1.0, 2.0, 3.0]]), requires_grad=True)# 多分類標簽 one-hot格式label = Variable(torch.zeros((3, 3)))label[0, 2] = 1label[1, 1] = 1label[2, 0] = 1print(label)# for batch loss = mean( -sum(Pj*logSj) )# for one : loss = -sum(Pj*logSj)loss = torch.mean(-torch.sum(label * torch.log(F.softmax(data, dim=1)), dim=1))loss.backward()print(loss, data.grad) |
輸出:
|
1
2
3
4
5
6
7
|
tensor([[ 0., 0., 1.], [ 0., 1., 0.], [ 1., 0., 0.]])# loss:損失 和 input's grad:輸入的梯度tensor(1.4076) tensor([[ 0.0300, 0.0816, -0.1116], [ 0.0300, -0.2518, 0.2217], [-0.3033, 0.0816, 0.2217]]) |
注意:
對于單輸入的loss 和 grad
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
data = Variable(torch.FloatTensor([[1.0, 2.0, 3.0]]), requires_grad=True)label = Variable(torch.zeros((1, 3)))#分別令不同索引位置label為1label[0, 0] = 1# label[0, 1] = 1# label[0, 2] = 1print(label)# for batch loss = mean( -sum(Pj*logSj) )# for one : loss = -sum(Pj*logSj)loss = torch.mean(-torch.sum(label * torch.log(F.softmax(data, dim=1)), dim=1))loss.backward()print(loss, data.grad) |
其輸出:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
# 第一組:lable: tensor([[ 1., 0., 0.]])loss: tensor(2.4076) grad: tensor([[-0.9100, 0.2447, 0.6652]])# 第二組:lable: tensor([[ 0., 1., 0.]])loss: tensor(1.4076) grad: tensor([[ 0.0900, -0.7553, 0.6652]])# 第三組:lable: tensor([[ 0., 0., 1.]])loss: tensor(0.4076) grad: tensor([[ 0.0900, 0.2447, -0.3348]])"""解釋:對于輸入數據 tensor([[ 1., 2., 3.]]) softmax之后的結果如下tensor([[ 0.0900, 0.2447, 0.6652]])交叉熵求解梯度推導公式可知 s[0, 0]-1, s[0, 1]-1, s[0, 2]-1 是上面三組label對應的輸入數據梯度""" |
pytorch提供的softmax, 和log_softmax 關系
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
# 官方提供的softmax實現In[2]: import torch ...: import torch.autograd as autograd ...: from torch.autograd import Variable ...: import torch.nn.functional as F ...: import torch.nn as nn ...: import numpy as npIn[3]: data = Variable(torch.FloatTensor([[1.0, 2.0, 3.0]]), requires_grad=True)In[4]: dataOut[4]: tensor([[ 1., 2., 3.]])In[5]: e = torch.exp(data)In[6]: eOut[6]: tensor([[ 2.7183, 7.3891, 20.0855]])In[7]: s = torch.sum(e, dim=1)In[8]: sOut[8]: tensor([ 30.1929])In[9]: softmax = e/sIn[10]: softmaxOut[10]: tensor([[ 0.0900, 0.2447, 0.6652]])In[11]: # 等同于 pytorch 提供的 softmax In[12]: org_softmax = F.softmax(data, dim=1)In[13]: org_softmaxOut[13]: tensor([[ 0.0900, 0.2447, 0.6652]])In[14]: org_softmax == softmax # 計算結果相同Out[14]: tensor([[ 1, 1, 1]], dtype=torch.uint8)# 與log_softmax關系# log_softmax = log(softmax)In[15]: _log_softmax = torch.log(org_softmax) In[16]: _log_softmaxOut[16]: tensor([[-2.4076, -1.4076, -0.4076]])In[17]: log_softmax = F.log_softmax(data, dim=1)In[18]: log_softmaxOut[18]: tensor([[-2.4076, -1.4076, -0.4076]]) |
官方提供的softmax交叉熵求解結果
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
# -*- coding: utf-8 -*-import torchimport torch.autograd as autogradfrom torch.autograd import Variableimport torch.nn.functional as Fimport torch.nn as nnimport numpy as npdata = Variable(torch.FloatTensor([[1.0, 2.0, 3.0], [1.0, 2.0, 3.0], [1.0, 2.0, 3.0]]), requires_grad=True)log_softmax = F.log_softmax(data, dim=1)label = Variable(torch.zeros((3, 3)))label[0, 2] = 1label[1, 1] = 1label[2, 0] = 1print("lable: ", label)# 交叉熵的計算方式之一loss_fn = torch.nn.NLLLoss() # reduce=True loss.sum/batch & grad/batch# NLLLoss輸入是log_softmax, target是非one-hot格式的labelloss = loss_fn(log_softmax, torch.argmax(label, dim=1))loss.backward()print("loss: ", loss, "\ngrad: ", data.grad)"""# 交叉熵計算方式二loss_fn = torch.nn.CrossEntropyLoss() # the target label is NOT an one-hotted#CrossEntropyLoss適用于分類問題的損失函數#input:沒有softmax過的nn.output, target是非one-hot格式labelloss = loss_fn(data, torch.argmax(label, dim=1))loss.backward()print("loss: ", loss, "\ngrad: ", data.grad)"""""" |
輸出
|
1
2
3
4
5
6
7
|
lable: tensor([[ 0., 0., 1.], [ 0., 1., 0.], [ 1., 0., 0.]])loss: tensor(1.4076) grad: tensor([[ 0.0300, 0.0816, -0.1116], [ 0.0300, -0.2518, 0.2217], [-0.3033, 0.0816, 0.2217]]) |
通過和示例的輸出對比, 發現兩者是一樣的
以上這篇PyTorch的SoftMax交叉熵損失和梯度用法就是小編分享給大家的全部內容了,希望能給大家一個參考,也希望大家多多支持服務器之家。
原文鏈接:https://blog.csdn.net/u010472607/article/details/82705567