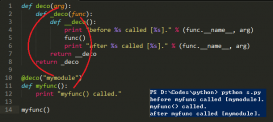
本文實(shí)例講述了python中尾遞歸用法。分享給大家供大家參考。具體分析如下:
如果一個(gè)函數(shù)中所有遞歸形式的調(diào)用都出現(xiàn)在函數(shù)的末尾,我們稱這個(gè)遞歸函數(shù)是尾遞歸的。當(dāng)遞歸調(diào)用是整個(gè)函數(shù)體中最后執(zhí)行的語(yǔ)句且它的返回值不屬于表達(dá)式的一部分時(shí),這個(gè)遞歸調(diào)用就是尾遞歸。尾遞歸函數(shù)的特點(diǎn)是在回歸過(guò)程中不用做任何操作,這個(gè)特性很重要,因?yàn)榇蠖鄶?shù)現(xiàn)代的編譯器會(huì)利用這種特點(diǎn)自動(dòng)生成優(yōu)化的代碼。
原理:
當(dāng)編譯器檢測(cè)到一個(gè)函數(shù)調(diào)用是尾遞歸的時(shí)候,它就覆蓋當(dāng)前的活躍記錄而不是在棧中去創(chuàng)建一個(gè)新的。編譯器可以做到這點(diǎn),因?yàn)檫f歸調(diào)用是當(dāng)前活躍期內(nèi)最后一條待執(zhí)行的語(yǔ)句,于是當(dāng)這個(gè)調(diào)用返回時(shí)棧幀中并沒(méi)有其他事情可做,因此也就沒(méi)有保存棧幀的必要了。通過(guò)覆蓋當(dāng)前的棧幀而不是在其之上重新添加一個(gè),這樣所使用的棧空間就大大縮減了,這使得實(shí)際的運(yùn)行效率會(huì)變得更高。因此,只要有可能我們就需要將遞歸函數(shù)寫(xiě)成尾遞歸的形式.
代碼:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
# This program shows off a python decorator(# which implements tail call optimization. It# does this by throwing an exception if it is# it's own grandparent, and catching such# exceptions to recall the stack.import sysclass TailRecurseException: def __init__(self, args, kwargs): self.args = args self.kwargs = kwargsdef tail_call_optimized(g): """ This function decorates a function with tail call optimization. It does this by throwing an exception if it is it's own grandparent, and catching such exceptions to fake the tail call optimization. This function fails if the decorated function recurses in a non-tail context. """ def func(*args, **kwargs): f = sys._getframe() if f.f_back and f.f_back.f_back and f.f_back.f_back.f_code == f.f_code: raise TailRecurseException(args, kwargs) else: while 1: try: return g(*args, **kwargs) except TailRecurseException, e: args = e.args kwargs = e.kwargs func.__doc__ = g.__doc__ return func@tail_call_optimizeddef factorial(n, acc=1): "calculate a factorial" if n == 0: return acc return factorial(n-1, n*acc)print factorial(10000)# prints a big, big number,# but doesn't hit the recursion limit.@tail_call_optimizeddef fib(i, current = 0, next = 1): if i == 0: return current else: return fib(i - 1, next, current + next)print fib(10000)# also prints a big number,# but doesn't hit the recursion limit. |
希望本文所述對(duì)大家的Python程序設(shè)計(jì)有所幫助。