本章先講解Java隨機數的幾種產生方式,然后通過示例對其進行演示。
概述:
這里你是不是會說,生成隨機數有什么難的?不就是直接使用Java封裝好了的random就行了么?當然對于一般情況下是OK的,而且本文要說明的這些算法也是基于這個random庫函數的。
本文主要是針對抽樣這一行為進行的,而抽樣本身有一個隱含的規則就是不要有重復數據。好了,有了這些說明。你可以先嘗試著用一些自己的想法來實現不重復地生成隨機數。
算法嘗試:
一些好的算法出現,往往伴隨著一些不那么好的算法。但是對于效果不太好的算法,它們普遍有一個共性,方便理解和實現。下面是通過一個循序漸進的方式來作一個簡單地說明。
第一次嘗試:樸素隨機算法
這個算法很好理解,就是隨機!每一次產生一個隨機數,并加入集合。
|
1
2
3
4
5
6
7
8
9
10
|
private void simpleRandom(int start, int end, int count) { System.out.println("樸素隨機算法:"); StringBuffer buffer = new StringBuffer(); for (int i = 0; i < count; i++) { int random = NumberUtils.randomInteger(start, end); buffer.append(i == 0 ? ("[" + random) : (", " + random)); } buffer.append("]"); System.out.println(buffer); } |
第二次嘗試:檢查存在性隨機算法
我們知道上面的方法有一個問題,就是可能會有重復數據。于是,我們就想到,在生成一個隨機數的時候進行檢查一下這個數是不是已經存在了,如果存在了就重新生成。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
private void checkRandom(int start, int end, int count) { System.out.println("檢查存在性隨機算法:"); StringBuffer buffer = new StringBuffer(); List<Integer> save = new ArrayList<>(); for (int i = 0; i < count; i++) { int random = NumberUtils.randomInteger(start, end); if (exits(save, random)) { i--; continue; } save.add(random); buffer.append(i == 0 ? ("[" + random) : (", " + random)); } buffer.append("]"); System.out.println(buffer); } |
第三次嘗試:元素移除隨機算法
上面的算法已經解決了數據重復的問題。不過,有一個很糟糕的問題就是可能我們要花費很長的時間來生成抽樣隨機數(這個要看臉了。。。。)。
不過,這里我們有了新想法。那就是在一個集合中去隨機一個數,當這個被選中的時候就remove掉,那么下次再隨機的時候是不是就不會再隨機到這個數了?這樣就很好地解決了隨機數的重復問題。代碼如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
private void removeRandom(int start, int end, int count) { System.out.println("元素移除隨機算法:"); StringBuffer buffer = new StringBuffer(); List<Integer> numbers = initList(start, end); for (int i = 0; i < count; i++) { int random = NumberUtils.randomInteger(count - i); buffer.append(i == 0 ? ("[" + numbers.get(random)) : (", " + numbers.get(random))); numbers.remove(random); } buffer.append("]"); System.out.println(buffer); } |
第四次嘗試:狀態轉移隨機算法
在我之前的很多博客中,就有一些是算法中的狀態轉移過程。而狀態的轉移也是我最喜歡的算法之一。下面的圖-1中標注了隨機數的取值范圍,序列中的橙色數字是結果中的隨機序列。最下方的序列中有一些虛線的箭頭,代表了狀態的轉移。
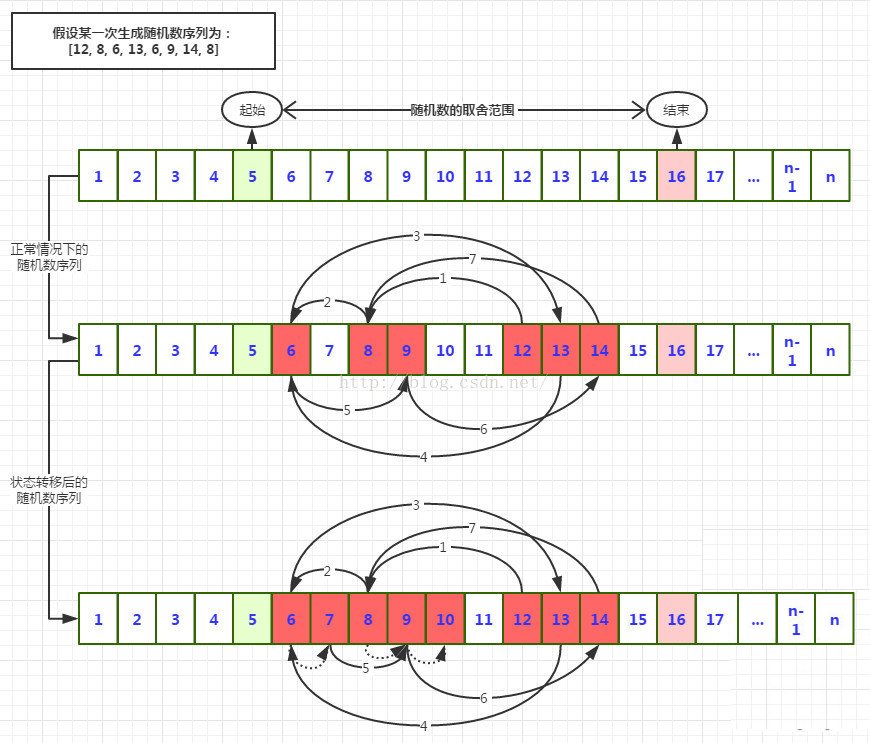
圖-1 基于狀態轉移的抽樣隨機數生成算法
實現代碼:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
private void statusRandom(int start, int end, int count) { System.out.println("狀態轉移隨機算法:"); StringBuffer buffer = new StringBuffer(); int[] status = new int[end + 1]; for (int i = 0; i < count; i++) { int random = NumberUtils.randomInteger(start, end); System.err.println(random); if (status[random] == 0) { buffer.append(i == 0 ? ("[" + random) : (", " + random)); status[random] = random == end ? start : (random + 1); // 不可能有在start之前的數字 } else { // 狀態轉移 int index = random; do { index = status[index]; } while (status[index] != 0); buffer.append(i == 0 ? ("[" + index) : (", " + index)); status[index] = index == end ? start : (index + 1); // 不可能有在start之前的數字 } } buffer.append("]"); System.out.println(buffer); } |
第五次嘗試:遞歸Floyd隨機算法
Floyd算法說到底也是一種狀態的轉移過程。該算法會要求輸入一個List或是array來保存已經確定的隨機數。顧名思義,這里我會用到遞歸的解法。在遞歸的過程中,我們把第i個隨機數的狀態轉移到了第i-1個隨機身上了。代碼如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
private List<Integer> simpleFloyd(List<Integer> list, int count, int start, int end) { if (count == 0) { return list; } list = simpleFloyd(list, count - 1, start, end - 1); int random = NumberUtils.randomInteger(start, end); if (list.contains(random)) { list.add(end); } else { list.add(random); } return list; } |
第六次嘗試:迭代Floyd隨機算法
思路與上面的遞歸Floyd隨機算法是相似的,不過,這里我們加入了一個變量來做優化。就不需要再去遞歸了。代碼如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
private List<Integer> iterationFloyd(int start, int end, int count) { System.out.println("迭代Floyd隨機算法:"); List<Integer> list = new ArrayList<>(); for (int i = end - count + 1; i < end; i++) { int random = NumberUtils.randomInteger(start, i); if (list.contains(random)) { list.add(i); } else { list.add(random); } } return list; } |
測試結果:

圖-2 隨機數生成算法測試結果
在上面的測試結果中,我們可以很明顯地看出樸素隨機算法不僅有重復數據,而且還是最耗時的。所以,在抽樣的隨機數生成時,避免使用這一算法。而在后幾種算法中,狀態轉移隨機算法最佳,迭代Floyd隨機算法次之。這個可以根據個人偏愛來做選擇。














