本來就是基礎知識,不能丟的太干凈,今天竟然花了那么長的時間才寫出來,記一下。
有如下的一顆完全二叉樹:
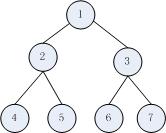
先序遍歷結果應該為:1 2 4 5 3 6 7
中序遍歷結果應該為:4 2 5 1 6 3 7
后序遍歷結果應該為:4 5 2 6 7 3 1
層序遍歷結果應該為:1 2 3 4 5 6 7
二叉樹的先序遍歷、中序遍歷、后序遍歷其實都是一樣的,都是執行遞歸操作。
我這記錄一下層次遍歷吧:層次遍歷需要用到隊列,先入隊在出隊,每次出隊的元素檢查是其是否有左右孩子,有則將其加入隊列,由于利用隊列的先進先出原理,進行層次遍歷。
下面記錄下完整代碼(Java實現),包括幾種遍歷方法:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
|
import java.util.ArrayDeque;import java.util.ArrayList;import java.util.List;import java.util.Queue;/** * 定義二叉樹節點元素 * @author bubble * */class Node { public Node leftchild; public Node rightchild; public int data; public Node(int data) { this.data = data; }}public class TestBinTree { /** * 將一個arry數組構建成一個完全二叉樹 * @param arr 需要構建的數組 * @return 二叉樹的根節點 */ public Node initBinTree(int[] arr) { if(arr.length == 1) { return new Node(arr[0]); } List<Node> nodeList = new ArrayList<>(); for(int i = 0; i < arr.length; i++) { nodeList.add(new Node(arr[i])); } int temp = 0; while(temp <= (arr.length - 2) / 2) { //注意這里,數組的下標是從零開始的 if(2 * temp + 1 < arr.length) { nodeList.get(temp).leftchild = nodeList.get(2 * temp + 1); } if(2 * temp + 2 < arr.length) { nodeList.get(temp).rightchild = nodeList.get(2 * temp + 2); } temp++; } return nodeList.get(0); } /** * 層序遍歷二叉樹,,并分層打印 * @param root 二叉樹根節點 * */ public void trivalBinTree(Node root) { Queue<Node> nodeQueue = new ArrayDeque<>(); nodeQueue.add(root); Node temp = null; int currentLevel = 1; //記錄當前層需要打印的節點的數量 int nextLevel = 0;//記錄下一層需要打印的節點的數量 while ((temp = nodeQueue.poll()) != null) { if (temp.leftchild != null) { nodeQueue.add(temp.leftchild); nextLevel++; } if (temp.rightchild != null) { nodeQueue.add(temp.rightchild); nextLevel++; } System.out.print(temp.data + " "); currentLevel--; if(currentLevel == 0) { System.out.println(); currentLevel = nextLevel; nextLevel = 0; } } } /** * 先序遍歷 * @param root 二叉樹根節點 */ public void preTrival(Node root) { if(root == null) { return; } System.out.print(root.data + " "); preTrival(root.leftchild); preTrival(root.rightchild); } /** * 中序遍歷 * @param root 二叉樹根節點 */ public void midTrival(Node root) { if(root == null) { return; } midTrival(root.leftchild); System.out.print(root.data + " "); midTrival(root.rightchild); } /** * 后序遍歷 * @param root 二叉樹根節點 */ public void afterTrival(Node root) { if(root == null) { return; } afterTrival(root.leftchild); afterTrival(root.rightchild); System.out.print(root.data + " "); } public static void main(String[] args) { TestBinTree btree = new TestBinTree(); int[] arr = new int[] {1,2,3,4,5,6,7}; Node root = btree.initBinTree(arr); System.out.println("層序遍歷(分層打印):"); btree.trivalBinTree(root); System.out.println("\n先序遍歷:"); btree.preTrival(root); System.out.println("\n中序遍歷:"); btree.midTrival(root); System.out.println("\n后序遍歷:"); btree.afterTrival(root); } } |
遍歷結果:

以上就是本文的全部內容,希望對大家的學習有所幫助,也希望大家多多支持服務器之家。
原文鏈接:http://www.cnblogs.com/gonjan-blog/p/6504668.html