線性表是其組成元素間具有線性關系的一種數據結構,對線性表的基本操作主要有,獲取元素,設置元素值,遍歷,插入,刪除,查找,替換,排序等。而線性表可以采用順序儲存結構和鏈式儲存結構,本節主要講解順序表、單鏈表以及雙鏈表的各種基本操作。
1:線性表抽象的數據類型
線性表:是由n(n>=0)個數據相同的元素組成的有限序列。線性表的定義接口如下
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
|
public interface ilist<t> { /** * 是否為空 * @return */ boolean isempty(); /** * 表的長度 * @return */ int length(); /** * 根據索引獲取長度 * @param i * @return */ t get(int i); /** * 設置第i個元素值為x * @param i * @param x */ void set(int i,t x); /** * 在線性表最后插入x元素 * @param x */ void append(t x); /** * 異常第i個元素并返回值 * @param i * @return */ t remove(int i); /** * 刪除線性表中所有元素 */ void removeall(); /** * 查詢首次出現關鍵字為key的元素 * @param key * @return */ t search(t key); void insert(int i,t x); /** * 升序添加 * @param x */ void insert(t x); /** * 升序刪除 * @param x */ void remove(t x);} |
2:線性表順序表示和實現
線性表的順序存儲結構是一組連續的內存單元依次存放的線性表的數據元素,元素的物理地址和邏輯地址次序是相同的。我們叫做這種存儲方式為順序表。
由于數組只能進行賦值和取值,而且長度是不可變化的,所以給我們的操作帶來很大的麻煩,但是用順序表就可以進行刪除,插入等操作。其實順序表內部同樣適用數組來表示的,只不過這個數據我們可以改變他的長度,這樣說來我們就好辦了,首先我們要為順序表定義一個數組,同時在定義一個值來記錄線性表的長度,所以第一步我們就有了如下

準備事件做好了以后,我們肯定會對順序表進行初始化,剛剛開始數組的長度肯定是0。但是我們必須要為數組開辟一個內存空間,來存儲要插入的元素,如下
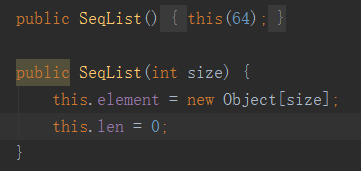
其他的都比較簡單,我主要說下插入和刪除
插入一個元素的時候,如果插在第i個位置,那么意味著它后面所有的元素前部往后面移一位,但是我們必須把i個位置留出來給即將插入的元素。但是我們還必須考慮,如果這個數組滿了的情況。如果滿了,我們必須重新為順序表開辟內存空間,然后把以前的元素進行遷移到新的表中,java實現如下
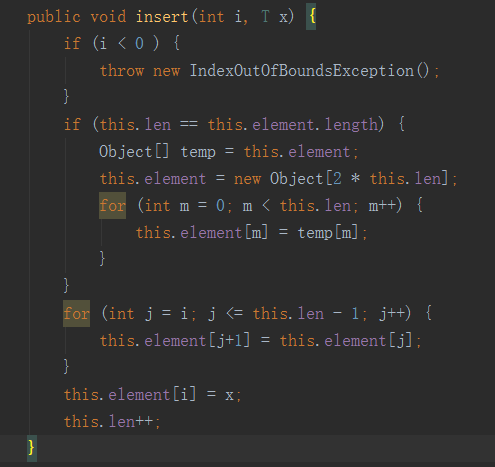
代碼看出,我們把從第i個位置的元素全部往后移(包括第i個元素)然后在把第i個元素進行賦值
刪除第i個元素,這個和上面的正好相反,如果刪除第i個元素意味著在i之后的元素前部往前移一位。
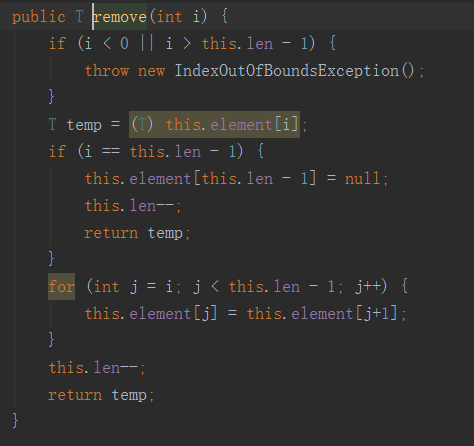
3:順序表操作效率分析
因為順序表是具有索引的,所以get()和set()效率極高,時間復雜度都是o(n)。
從上面發現,在插入和刪除的時候都是需要大量元素的移動,因為在各個位置插入元素的概率相同,所以平均插入一個元素要移動的元素是2/n。那么它的時間復雜度就是o(n),如果要容器滿了,那么就需要申請更大的容器來存儲新加入的元素,那么效率會更加的低下。所以順序表的靜態性好,動態性就很差了,所以在選擇的時候就要注意一下。
4:單鏈表的實現
線性表的鏈式存儲結構是用若干地址分散的存儲單元存儲數據元素,邏輯上相鄰的2個元素,物理地址不一定相同,這么說來就充分的利用了內存中的地址。但是我們必須用附加信息來連接2個不同的數據元素,所以這里就引進了2個概念,數據域(data)和地址域(next),其中數據域存儲的是這個元素的值,地址域存儲下一個元素的地址。其中數據域和地址域聯合起來我們稱為節點(node)。如果只有后繼節點沒有前驅節點我們就稱為單鏈表,那么現在我們來看看單鏈表的實現。
首先我們要定義一個節點node
|
1
2
3
4
5
6
7
8
9
10
11
|
public class node<t> { public t data;//數據域 public node next;//地址域 public node() { this(null, null); } public node(t data, node next) { this.data = data; this.next = next; }} |
現在我們想象一下,a(x)和b(y)2個節點,其中a的后繼節點是b,那么我們怎么表示呢,如下
|
1
2
3
|
node<string> a=new node<t>(x,null);node<string> b=new node<t>(y,null);a.next=b。 |
也可以把a寫成node<string> a=new node<t>(x,b);
ok現在我們正式開始實現一個帶有頭節點的單鏈表
我們可以把頭指針想象成一個指針來便于我們的操作,我們先看如何實現單鏈表的長度
|
1
2
3
4
5
6
7
8
9
|
public int length() { int i = 0; node<t> p = this.head.next; while (p != null) { p = p.next; i++; } return i; } |
因為這是一個鏈式的結構,我們無法得知長度,只能通過循環來知道鏈表中節點的個數,因為頭指針的后繼節點就是我們鏈表中第一個節點,所以我們就可以這樣往下循環來得知。
獲取第i個節點的值
同樣我們無法直接獲取節點,這個時候同樣采用循環,如果循環第i個元素值等于我們i那么我們就獲取這個節點,然后得到值
|
1
2
3
4
5
6
7
8
9
10
11
12
|
public t get(int i) { if (i >= 0) { node<t> p = this.head; for (int j = 0; j <= i; j++) { p = p.next; } if (p!=null){ return p.data; } } return null; } |
在第i個位置插入一個節點
首先我們必須要找到要插入節點的前驅節點,然后前驅節點的后繼節點指向這個新節點,新節點的后繼節點指向原來前驅節點的后繼節點。
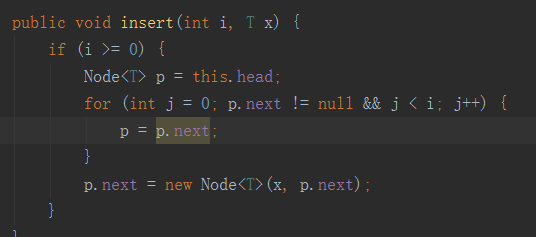
從代碼看出我們是根據頭節點進行循環的。加入p.next!=null的目的是為了當循環到最后一個節點的時候就停止,不在繼續了。
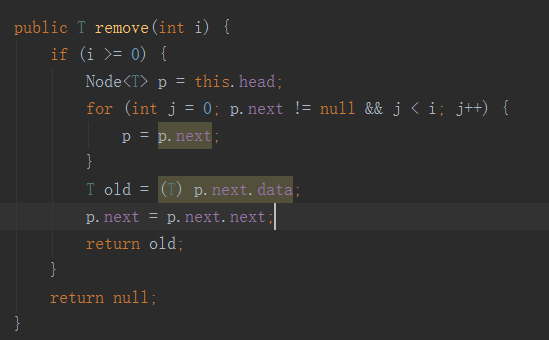
移除第i個節點
如果我們要刪除第i個節點和上面差不多,同樣我們要找到這個第i個節點的前驅節點,和上面代碼差不多。
在鏈表后追加一個節點。
如果傳統的話我們可以采取insert(this.length,x);但是這樣一來計算長度的時候就需要遍歷鏈表無疑速度減慢,只需要如下
insert(integer.max_value, x)即可,從插入代碼可以看到當循環到最后一個節點就不會繼續了,然后把新的節點加入最后即可。
5:排序單鏈表
排序首先我們需要我們的元素要繼承comparable。
我們就說插入和刪除。先說插入
如果插入一個元素,我們先獲取要插入這個節點的前驅節點和后繼節點。(x.compareto(y)<0 表示小于y)

其中p.data.next.compareto(x)<0如果跳出循環說明p節點值大于或等于x
如果刪除一個元素,和上面的基本一樣,但是要加上一個判斷如下

其中通過上面判斷我們知道p節點大于或等于x節點了,所以需要再次判斷。
6:單鏈表操作效率分析
單鏈表在獲取元素和設置元素的時候都需要進行遍歷所以時間復雜度o(n)
如果在p節點插入或刪除元素,只需要修改鏈的后繼節點的地址即可所以時間復雜度o(1),但是如果插入類似insert(i,x)就需要進行遍歷了,那么時間復雜度就是o(n).
對單鏈表進行插入和刪除只需要改變少量節點的鏈,不需要移動元素,單鏈表的插入和刪除都是動態申請和釋放的,不需要預先分配存儲空間,從而不會因為存儲空間不足而進行擴容,提高了運行效率。
7:雙鏈表的實現
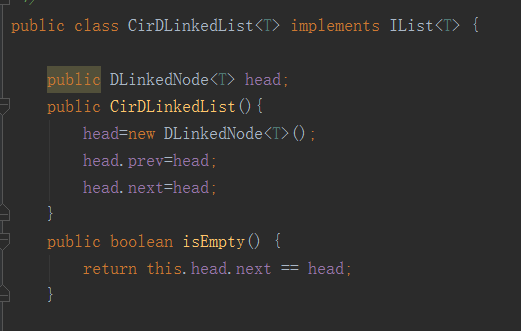
雙鏈表和單鏈表大多是相同的只不過多了前驅節點,現在我們先定義一下雙鏈表

我們這里來演示循環雙鏈表的實現。基本和單鏈表相同只不過如果為空鏈表那么它的后繼節點就是頭節點。ok我們先來看
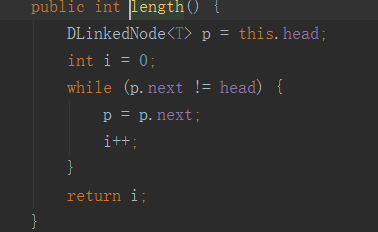
求雙鏈表的長度(基本和單鏈表一樣后面一樣的不在寫了)因為是循環雙鏈表最后一個節點的后繼節點為
我們這里只說插入和刪除(其他基本一樣和單鏈表)
插入
同樣我們需要找到要插入的節點
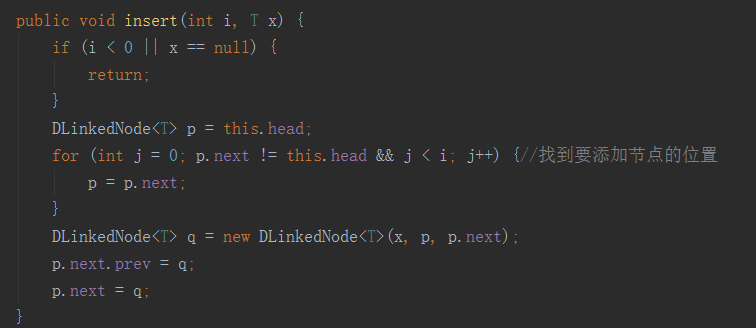
其中p.next!=this.head表示如果是最后一個節點則跳出循環。其中要插入的節點在p節點之后,然后我們就好理解了。
刪除
和上面的差不多

8:循環雙鏈表

根本和單鏈表一樣。也是先找到節點的位置然后插入或刪除
總結:主要是回顧一下線性表,通過對線性表的了解,在以后我們看java容器源碼的時候會帶來極大的幫助
以上就是本文的全部內容,希望本文的內容對大家的學習或者工作能帶來一定的幫助,同時也希望多多支持服務器之家!