一、插入類排序
1.直接插入排序
思想:將第i個插入到前i-1個中的適當位置
時間復雜度:t(n) = o(n²)。
空間復雜度:s(n) = o(1)。
穩定性:穩定排序。

如果碰見一個和插入元素相等的,那么插入元素把想插入的元素放在相等元素的后面。
所以,相等元素的前后順序沒有改變,從原無序序列出去的順序就是排好序后的順序,所以插入排序是穩定
哨兵有兩個作用:
① 進人查找(插入位置)循環之前,它保存了r[i]的副本,使不致于因記錄后移而丟失r[i]的內容;
② 它的主要作用是:在查找循環中"監視"下標變量j是否越界。一旦越界(即j=0),因為r[0].可以和自己比較,循環判定條件不成立使得查找循環結束,從而避免了在該循環內的每一次均要檢測j是否越界(即省略了循環判定條件"j>=1")
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
public void insertsort(int[] array){ for(int i=1;i<array.length;i++)//第0位獨自作為有序數列,從第1位開始向后遍歷 { if(array[i]<array[i-1])//0~i-1位為有序,若第i位小于i-1位,繼續尋位并插入,否則認為0~i位也是有序的,忽略此次循環,相當于continue { int temp=array[i];//保存第i位的值 int k = i - 1; for(int j=k;j>=0 && temp<array[j];j--)//從第i-1位向前遍歷并移位,直至找到小于第i位值停止 { array[j+1]=array[j]; k--; } array[k+1]=temp;//插入第i位的值 } }} |
2.折半插入排序
思想:將數據插入到已經排好序的序列中,通過不斷與中間點比較大小來確定位置
時間復雜度:比較時的時間減為o(n㏒n),但是移動元素的時間耗費未變,所以總是得時間復雜度還是o(n²)。
空間復雜度:s(n) = o(1)。
穩定性:穩定排序。
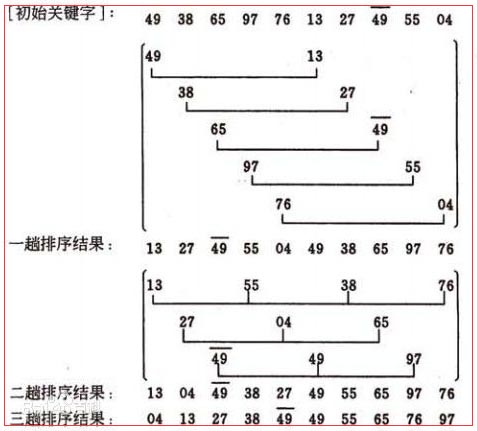
3.希爾排序
思想:又稱縮小增量排序法。把待排序序列分成若干較小的子序列,然后逐個使用直接插入排序法排序,最后再對一個較為有序的序列進行一次排序,主要是為了減少移動的次數,提高效率。原理應該就是從無序到漸漸有序,要比直接從無序到有序移動的次數會少一些。
時間復雜度:o(n的1.5次方)
空間復雜度:o(1)
穩定性:不穩定排序。{2,4,1,2},2和1一組4和2一組,進行希爾排序,第一個2和最后一個2會發生位置上的變化。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
public static void main(string [] args){ int[]a={49,38,65,97,76,13,27,49,78,34,12,64,1}; system.out.println("排序之前:"); for(int i=0;i<a.length;i++) { system.out.print(a[i]+" "); } //希爾排序 int d=a.length; while(true) { d=d/2; for(int x=0;x<d;x++) { for(int i=x+d;i<a.length;i=i+d) { int temp=a[i]; int j; for(j=i-d;j>=0&&a[j]>temp;j=j-d) { a[j+d]=a[j]; } a[j+d]=temp; } } if(d==1) { break; } } system.out.println(); system.out.println("排序之后:"); for(int i=0;i<a.length;i++) { system.out.print(a[i]+" "); } }} |
二、交換類排序
1.冒泡排序
時間復雜度:t(n) = o(n²)。
空間復雜度:s(n) = o(1)。
穩定性:穩定排序。

|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
public class bubblesort{ public void sort(int[] a) { int temp = 0; for (int i = a.length - 1; i > 0; --i) { for (int j = 0; j < i; ++j) { if (a[j + 1] < a[j]) { temp = a[j]; a[j] = a[j + 1]; a[j + 1] = temp; } } } }} |
2.快速排序
思想:對冒泡排序的改進,通過一趟排序將要排序的數據分割成獨立的兩部分,其中一部分的所有數據都比另外一部分的所有數據都要小,然后再按此方法對這兩部分數據分別進行快速排序,整個排序過程可以遞歸進行,以此達到整個數據變成有序序列。
時間復雜度:平均t(n) = o(n㏒n),最壞o(n²)。
空間復雜度:s(n) = o(㏒n)。
穩定性:不穩定排序
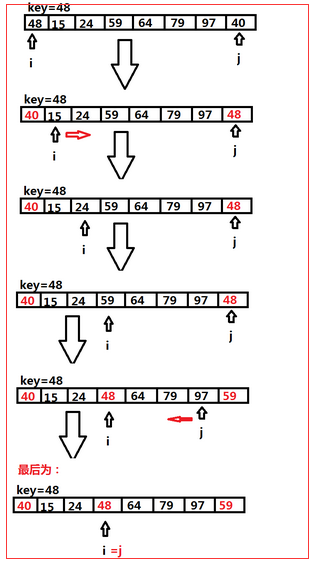
首先把數組的第一個數拿出來做為一個key,在前后分別設置一個i,j做為標識,然后拿這個key對這個數組從后面往前遍歷,及j--,直到找到第一個小于這個key的那個數,然后交換這兩個值,交換完成后,我們拿著這個key要從i往后遍歷了,及i++;一直循環到i=j結束,當這里結束后,我們會發現大于這個key的值都會跑到這個key的后面
三、選擇類排序
1.簡單選擇排序
時間復雜度:t(n) = o(n²)。
空間復雜度:s(n) = o(1)。
穩定性:不穩定排序
思路:
1)從待排序的序列中,找到關鍵字最小的元素
2)如果最小的元素不在第一位,就和第一個元素互換位置
3)從余下的n-1個元素中,找到關鍵字最小的元素,重復 1)、2)步

|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
public class selectionsort { public void selectionsort(int[] list) { // 需要遍歷獲得最小值的次數 // 要注意一點,當要排序 n 個數,已經經過 n-1 次遍歷后,已經是有序數列 for (int i = 0; i < list.length - 1; i++) { int temp = 0; int index = i; // 用來保存最小值得索引 // 尋找第i個小的數值 for (int j = i + 1; j < list.length; j++) { if (list[index] > list[j]) { index = j; } } // 將找到的第i個小的數值放在第i個位置上 temp = list[index]; list[index] = list[i]; list[i] = temp; system.out.format("第 %d 趟:\t", i + 1); printall(list); } } // 打印完整序列 public void printall(int[] list) { for (int value : list) { system.out.print(value + "\t"); } system.out.println(); } public static void main(string[] args) { // 初始化一個隨機序列 final int max_size = 10; int[] array = new int[max_size]; random random = new random(); for (int i = 0; i < max_size; i++) { array[i] = random.nextint(max_size); } // 調用排序方法 selectionsort selection = new selectionsort(); system.out.print("排序前:\t"); selection.printall(array); selection.selectionsort(array); system.out.print("排序后:\t"); selection.printall(array); }} |
2.樹形選擇排序
思想:為了減少比較次數,兩兩進行比較,得出的較小的值再兩兩比較,直至得出最小的輸出,然后在原來位置上置為∞,再進行比較。直至所有都輸出。
時間復雜度:t(n) = o(n㏒n)。
空間復雜度:較簡單選擇排序,增加了n-1個額外的存儲空間存放中間比較結果,就是樹形結構的所有根節點。s(n) = o(n)。
穩定性:穩定排序。
3.堆排序
【待】
四.、歸并排序
歸并排序:
思想:假設初始序列有n個記錄,首先將這n個記錄看成n個有序的子序列,每個子序列的長度為1,然后兩兩歸并,得到n/2向上取整個長度為2(n為奇數時,最后一個序列的長度為1)的有序子序列
在此基礎上,在對長度為2的有序子序列進行兩兩歸并,得到若干個長度為4的有序子序列
如此重復,直至得到一個長度為n的有序序列為止。
時間復雜度:t(n) = o(n㏒n)
空間復雜度:s(n) = o(n)
穩定性:穩定排序

|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
public class mergesort { public static void merge(int[] a, int low, int mid, int high) { int[] temp = new int[high - low + 1]; int i = low;// 左指針 int j = mid + 1;// 右指針 int k = 0; // 把較小的數先移到新數組中 while (i <= mid && j <= high) { if (a[i] < a[j]) { temp[k++] = a[i++]; } else { temp[k++] = a[j++]; } } // 把左邊剩余的數移入數組 while (i <= mid) { temp[k++] = a[i++]; } // 把右邊邊剩余的數移入數組 while (j <= high) { temp[k++] = a[j++]; } // 把新數組中的數覆蓋nums數組 for (int k2 = 0; k2 < temp.length; k2++) { a[k2 + low] = temp[k2]; } } public static void mergesort(int[] a, int low, int high) { int mid = (low + high) / 2; if (low < high) { // 左邊 mergesort(a, low, mid); // 右邊 mergesort(a, mid + 1, high); // 左右歸并 merge(a, low, mid, high); system.out.println(arrays.tostring(a)); } } public static void main(string[] args) { int a[] = { 51, 46, 20, 18, 65, 97, 82, 30, 77, 50 }; mergesort(a, 0, a.length - 1); system.out.println("排序結果:" + arrays.tostring(a)); }} |
五、分配類排序
1.多關鍵字排序:
【待】
2.鏈式基數排序:
思想:先分配,再收集,就是先按照一個次關鍵字收集一下,然后進行收集(第一個排序),然后再換一個關鍵字把新序列分配一下,然后再收集起來,又完成一次排序,這樣所有關鍵字分配收集完后,就完成了排序。
時間復雜度:t(n) = o( d ( n + rd ) )
空間復雜度:s(n) = o(rd)
穩定性:穩定排序
以上這篇詳細總結各種排序算法(java實現)就是小編分享給大家的全部內容了,希望能給大家一個參考,也希望大家多多支持服務器之家。
原文鏈接:http://www.cnblogs.com/lwj-0923/archive/2017/09/11/7487432.html