本文實例講述了java完全二叉樹的創建與四種遍歷方法。分享給大家供大家參考,具體如下:
有如下的一顆完全二叉樹:

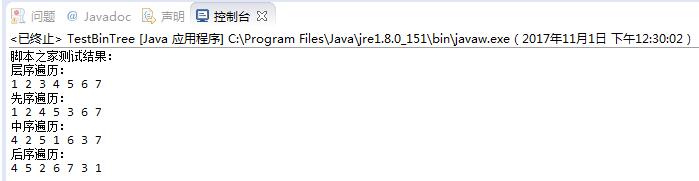
先序遍歷結果應該為:1 2 4 5 3 6 7
中序遍歷結果應該為:4 2 5 1 6 3 7
后序遍歷結果應該為:4 5 2 6 7 3 1
層序遍歷結果應該為:1 2 3 4 5 6 7
二叉樹的先序遍歷、中序遍歷、后序遍歷其實都是一樣的,都是執行遞歸操作。
我這記錄一下層次遍歷吧:層次遍歷需要用到隊列,先入隊在出隊,每次出隊的元素檢查是其是否有左右孩子,有則將其加入隊列,由于利用隊列的先進先出原理,進行層次遍歷。
下面記錄下完整代碼(java實現),包括幾種遍歷方法:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
|
import java.util.arraydeque;import java.util.arraylist;import java.util.list;import java.util.queue;/** * 定義二叉樹節點元素 * @author bubble * */class node { public node leftchild; public node rightchild; public int data; public node(int data) { this.data = data; }}public class testbintree { /** * 將一個arry數組構建成一個完全二叉樹 * @param arr 需要構建的數組 * @return 二叉樹的根節點 */ public node initbintree(int[] arr) { if(arr.length == 1) { return new node(arr[0]); } list<node> nodelist = new arraylist<>(); for(int i = 0; i < arr.length; i++) { nodelist.add(new node(arr[i])); } int temp = 0; while(temp <= (arr.length - 2) / 2) { //注意這里,數組的下標是從零開始的 if(2 * temp + 1 < arr.length) nodelist.get(temp).leftchild = nodelist.get(2 * temp + 1); if(2 * temp + 2 < arr.length) nodelist.get(temp).rightchild = nodelist.get(2 * temp + 2); temp++; } return nodelist.get(0); } /** * 層序遍歷二叉樹 * @param root 二叉樹根節點 * @param nodequeue ,用到的隊列數據結構 */ public void trivalbintree(node root, queue<node> nodequeue) { nodequeue.add(root); node temp = null; while ((temp = nodequeue.poll()) != null) { system.out.print(temp.data + " "); if (temp.leftchild != null) { nodequeue.add(temp.leftchild); } if (temp.rightchild != null) { nodequeue.add(temp.rightchild); } } } /** * 先序遍歷 * @param root 二叉樹根節點 */ public void pretrival(node root) { if(root == null) { return; } system.out.print(root.data + " "); pretrival(root.leftchild); pretrival(root.rightchild); } /** * 中序遍歷 * @param root 二叉樹根節點 */ public void midtrival(node root) { if(root == null) { return; } midtrival(root.leftchild); system.out.print(root.data + " "); midtrival(root.rightchild); } /** * 后序遍歷 * @param root 二叉樹根節點 */ public void aftertrival(node root) { if(root == null) { return; } aftertrival(root.leftchild); aftertrival(root.rightchild); system.out.print(root.data + " "); } public static void main(string[] args) { testbintree btree = new testbintree(); int[] arr = new int[] {1,2,3,4,5,6,7}; node root = btree.initbintree(arr); queue<node> nodequeue = new arraydeque<>(); system.out.println("服務器之家測試結果:"); system.out.println("層序遍歷:"); btree.trivalbintree(root, nodequeue); system.out.println("\n先序遍歷:"); btree.pretrival(root); system.out.println("\n中序遍歷:"); btree.midtrival(root); system.out.println("\n后序遍歷:"); btree.aftertrival(root); }} |
運行結果:
附:滿二叉樹 與完全二叉樹的區別
滿二叉樹是指這樣的一種二叉樹:除最后一層外,每一層上的所有結點都有兩個子結點。在滿二叉樹中,每一層上的結點數都達到最大值,即在滿二叉樹的第k層上有2k-1個結點,且深度為m的滿二叉樹有2m-1個結點。
完全二叉樹是指這樣的二叉樹:除最后一層外,每一層上的結點數均達到最大值;在最后一層上只缺少右邊的若干結點。
對于完全二叉樹來說,葉子結點只可能在層次最大的兩層上出現:對于任何一個結點,若其右分支下的子孫結點的最大層次為p,則其左分支下的子孫結點的最大層次或為p,或為p+1。
完全二叉樹具有以下兩個性質:
性質5:具有n個結點的完全二叉樹的深度為[log2n]+1。
性質6:設完全二叉樹共有n個結點。如果從根結點開始,按層次(每一層從左到右)用自然數1,2,……,n給結點進行編號,則對于編號為k(k=1,2,……,n)的結點有以下結論:
①若k=1,則該結點為根結點,它沒有父結點;若k>1,則該結點的父結點編號為int(k/2)。
②若2k≤n,則編號為k的結點的左子結點編號為2k;否則該結點無左子結點(顯然也沒有右子結點)。
③若2k+1≤n,則編號為k的結點的右子結點編號為2k+1;否則該結點無右子結點。
滿二叉樹肯定是完全二叉樹,完全二叉樹不一定是滿二叉樹。
希望本文所述對大家java程序設計有所幫助。
原文鏈接:http://blog.csdn.net/u010091003/article/details/60349597