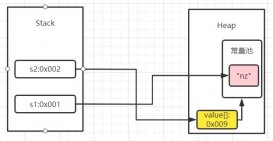
圖的概念
圖是算法中是樹的拓展,樹是從上向下的數據結構,結點都有一個父結點(根結點除外),從上向下排列。而圖沒有了父子結點的概念,圖中的結點都是平等關系,結果更加復雜。
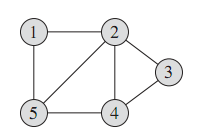
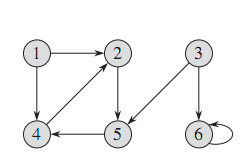
無向圖 有向圖
圖g=(v,e),其中v代表頂點vertex,e代表邊edge,一條邊就是一個定點對(u,v),其中(u,v)∈v。
這兩天遇到一個關于圖的算法,在網上找了很久沒有找到java版的關于數據結構中圖的存儲及其相關操作。于是找了一本java版的數據結構書看了一下,以下是根據書上的講解整理的一個關于無向圖的存儲和對圖的深度優先遍歷。不過這個遍歷只能遍歷連通圖,要想遍歷非連通圖,還需要修改。在這里分享一下代碼希望對有需要的人有幫助。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
|
package com.homework;/** * 定義棧類 */class stackx{ private final int size = 20; private int[] st; private int top; //初始化棧 public stackx(){ st = new int[size]; top = -1; } //進棧 public void push(int j){ st[++top] = j; } //出棧 public int pop(){ return st[top--]; } //返回棧頂元素 public int peak(){ return st[top]; } //判斷棧是否為空 public boolean isempty(){ return (top==-1); }}/** * 定義圖中的節點類 * @author administrator * */class vertex{ public char label; public boolean wasvisited; public vertex(char lab){ label = lab; wasvisited = false; }}/** * 定義圖類 * @author administrator * */class graph{ private final int num = 20; private vertex vertexlist[]; //圖中節點數組 private int adjmat[][]; //節點矩陣 private int nverts; //當前節點數 private stackx thestack; //定義一個棧 //初始化圖的結構 public graph(){ vertexlist = new vertex[num]; adjmat = new int[num][num]; nverts = 0; for (int i=0; i<num; i++){ for (int j=0; j<num; j++) adjmat[i][j] = 0; } } //添加節點 public void addvertex(char lab){ vertexlist[nverts++] = new vertex(lab); } //添加某兩個節點之間的邊 public void addedge(int start,int end){ adjmat[start][end] = 1; adjmat[end][start] = 1; } //輸出某個節點 public void displayvertex(int v){ system.out.print(vertexlist[v].label); } //獲取未被訪問的幾點 public int getadjunvisitedvertex(int v){ for (int j=0; j<nverts; j++){ if(adjmat[v][j]==1 && vertexlist[j].wasvisited==false) return j; } return -1; } //深度優先遍歷(dfs) public void dfs(){ vertexlist[0].wasvisited=true; displayvertex(0); thestack= new stackx(); thestack.push(0); while(!thestack.isempty()){ int v = getadjunvisitedvertex(thestack.peak()); if(v==-1)//若不存在該節點 thestack.pop(); else { vertexlist[v].wasvisited = true; displayvertex(v); thestack.push(v); } } for (int j=0; j<nverts; j++) vertexlist[j].wasvisited = false; }}public class graphconnect { public static void main(string[] args){ { graph thegraph = new graph(); thegraph.addvertex('a'); thegraph.addvertex('b'); thegraph.addvertex('c'); thegraph.addvertex('d'); thegraph.addvertex('e'); thegraph.addedge(0, 1); //ab thegraph.addedge(1, 2); //bc thegraph.addedge(0, 3); //ad thegraph.addedge(3, 4); //de thegraph.addedge(2, 4); //ce system.out.print("the order visited:"); thegraph.dfs(); system.out.println(); } }} |
程序運行的結果:
|
1
|
the order visited:abced |
總結
以上就是本文關于java編程無向圖結構的存儲及dfs操作代碼詳解的全部內容,希望對大家有所幫助。如有不足之處,歡迎留言指出。感謝朋友們對本站的支持!
原文鏈接:http://blog.csdn.net/sober_123/article/details/49716961