一晃工作有段時間了,第一次寫博客,有點不知道怎么寫,大家將就著看吧,說的有什么不正確的也請大家指正。
最近工作中用到了一個圖像壓縮的功能。找了一些工具,沒有太好的選擇。最后選了一個叫jdeli的,奈何效率又成了問題。我迫于無奈就只能研究了下它的源碼,卻發現自己對它的一個減色量化算法起了興趣,可是尷尬的自己完全不明白它寫的什么,就起了一個自己實現一個量化顏色算法的念頭。
自己找了一些資料,找到三個比較常用的顏色處理算法:
流行色算法:
具體的算法就是,先對一個圖像的所有顏色出現的次數進行統計,選舉出出現次數最多的256個顏色作為圖片的調色板的顏色,然后再次遍歷圖片的所有像素,對每個像素找出調色板中的最接近的顏色(這里我用的是方差的方式),寫回到圖片中。這個算法的實現比較簡單,但是失真比較嚴重,圖像中一些出現頻率較低,但對人眼的視覺效挺明顯的信息將丟失。比如,圖像中存在的高亮度斑點,由于出現的次數少,很可能不能被算法選中,將被丟失。
中位切分算法:
這個算法我沒有研究,想要了解的同學,可以看下這篇文章,里面有三種算法的介紹。
八叉樹
這個算法就是我最后選用的算法,它的主要思想就是把圖像的RGB顏色值轉成二進制分布到八叉樹中,例如:(173,234,144)
轉成二進制就是(10101101,11101010,10010000),將R,G,B的第一位取出來組成(111),作為root節點的子節點,其中111作為root子節點數組的索引,以此類推,一直到最后一位,然后在葉子節點上存放這個顏色的分量值以及其出現的次數。具體看圖。
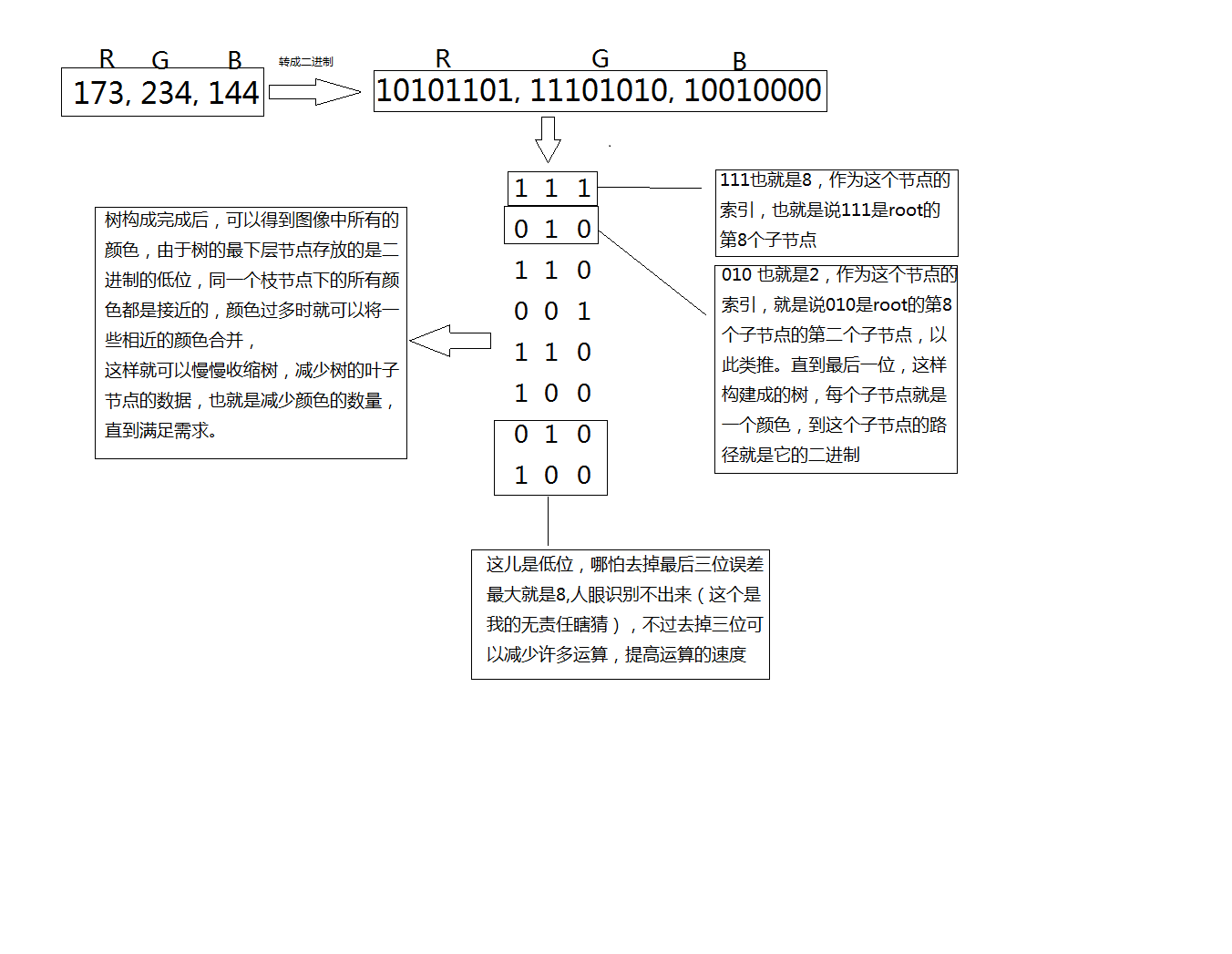
其中我比較疑惑的有一個處理就是葉子節點的合并策略,這兒我用的最笨的一個方法,就是找到層次最深的節點,然后合并,有點簡單粗暴,有別的比較好的方法,也請大家給我留言。圖片太大上傳不了了,直接上代碼了,代碼沒有重構,大家湊合看吧。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
|
package com.gys.pngquant.octree;import java.util.ArrayList;import java.util.HashMap;import java.util.List;import java.util.Map;/** * * * @ClassName 類名:Node * @Description 功能說明: * <p> * 八叉樹實現 * </p> * * 2015-12-16 guoys 創建該類功能。 * ********************************************************** * </p> */public class Node{ private int depth = 0; // 為0時為root節點 private Node parent; private Node[] children = new Node[8]; private Boolean isLeaf = false; private int rNum = 0; private int gNum = 0; private int bNum = 0; private int piexls = 0; private Map<Integer, List<Node>> levelMapping; // 存放層次和node的關系 public int getRGBValue(){ int r = this.rNum / this.piexls; int g = this.gNum / this.piexls; int b = this.bNum / this.piexls; return (r << 16 | g << 8 | b); } public Map<Integer, List<Node>> getLevelMapping() { return levelMapping; } public void afterSetParam(){ if(this.getParent() == null && this.depth == 0){ levelMapping = new HashMap<Integer, List<Node>>(); for (int i = 1; i <= 8; i++) { levelMapping.put(i, new ArrayList<Node>()); } } } public int getrNum() { return rNum; } public void setrNum(int rNum) { if(!isLeaf){ throw new UnsupportedOperationException(); } this.rNum = rNum; } public int getgNum() { return gNum; } public void setgNum(int gNum) { if(!isLeaf){ throw new UnsupportedOperationException(); } this.gNum = gNum; } public int getbNum() { return bNum; } public void setbNum(int bNum) { if(!isLeaf){ throw new UnsupportedOperationException(); } this.bNum = bNum; } public int getPiexls() { return piexls; } public void setPiexls(int piexls) { if(!isLeaf){ throw new UnsupportedOperationException(); } this.piexls = piexls; } public int getDepth() { return depth; } // 返回節點原有的子節點數量 public int mergerLeafNode(){ if(this.isLeaf){ return 1; } this.setLeaf(true); int rNum = 0; int gNum = 0; int bNum = 0; int pixel = 0; int i = 0; for (Node child : this.children) { if(child == null){ continue; } rNum += child.getrNum(); gNum += child.getgNum(); bNum += child.getbNum(); pixel += child.getPiexls(); i += 1; } this.setrNum(rNum); this.setgNum(gNum); this.setbNum(bNum); this.setPiexls(pixel); this.children = null; return i; } // 獲取最深層次的node public Node getDepestNode(){ for (int i = 7; i > 0; i--) { List<Node> levelList = this.levelMapping.get(i); if(!levelList.isEmpty()){ return levelList.remove(levelList.size() - 1); } } return null; } // 獲取葉子節點的數量 public int getLeafNum(){ if(isLeaf){ return 1; } int i = 0; for (Node child : this.children) { if(child != null){ i += child.getLeafNum(); } } return i; } public void setDepth(int depth) { this.depth = depth; } public Node getParent() { return parent; } public void setParent(Node parent) { this.parent = parent; } public Node[] getChildren() { return children; } public Node getChild(int index){ return children[index]; } public void setChild(int index, Node node){ children[index] = node; } public Boolean isLeaf() { return isLeaf; } public void setPixel(int r, int g, int b){ this.rNum += r; this.gNum += g; this.bNum += b; this.piexls += 1; } public void setLeaf(Boolean isLeaf) { this.isLeaf = isLeaf; } public void add8Bite2Root(int _taget, int _speed){ if(depth != 0 || this.parent != null){ throw new UnsupportedOperationException(); } int speed = 7 + 1 - _speed; int r = _taget >> 16 & 0xFF; int g = _taget >> 8 & 0xFF; int b = _taget & 0xFF; Node proNode = this; for (int i=7;i>=speed;i--){ int item = ((r >> i & 1) << 2) + ((g >> i & 1) << 1) + (b >> i & 1); Node child = proNode.getChild(item); if(child == null){ child = new Node(); child.setDepth(8-i); child.setParent(proNode); child.afterSetParam(); this.levelMapping.get(child.getDepth()).add(child); proNode.setChild(item, child); } if(i == speed){ child.setLeaf(true); } if(child.isLeaf()){ child.setPixel(r, g, b); break; } proNode = child; } } public static Node build(int[][] matrix, int speed){ Node root = new Node(); root.afterSetParam(); for (int[] row : matrix) { for (int cell : row) { root.add8Bite2Root(cell, speed); } } return root; } public static byte[] mergeColors(Node root, int maxColors){ byte[] byteArray = new byte[maxColors * 3]; List<byte> result = new ArrayList<byte>(); int leafNum = root.getLeafNum(); try{ while(leafNum > maxColors){ int mergerLeafNode = root.getDepestNode().mergerLeafNode(); leafNum -= (mergerLeafNode - 1); } } catch(Exception e){ e.printStackTrace(); } fillArray(root, result, 0); int i = 0; for (byte byte1 : result) { byteArray[i++] = byte1; } return byteArray; } private static void fillArray(Node node, List<byte> result, int offset){ if(node == null){ return; } if(node.isLeaf()){ result.add((byte) (node.getrNum() / node.getPiexls())); result.add((byte) (node.getgNum() / node.getPiexls())); result.add((byte) (node.getbNum() / node.getPiexls())); } else{ for (Node child : node.getChildren()) { fillArray(child, result, offset); } } }} |
可憐我大學唯二掛的數據結構。代碼實現的只是八叉樹,對一個1920*1080圖片量化,耗時大概是450ms,如果層次-2的話大概是100ms左右。
好吧,這篇就這樣吧,本來寫之前,感覺自己想說的挺多的,結果寫的時候就不知道怎么說了,大家見諒。
總結
以上就是本文關于java簡單實現八叉樹圖像處理代碼示例的全部內容,希望對大家有所幫助。感興趣的朋友可以繼續參閱本站其他相關專題,如有不足之處,歡迎留言指出。感謝朋友們對本站的支持!
原文鏈接:http://blog.csdn.net/u013206238/article/details/50328359