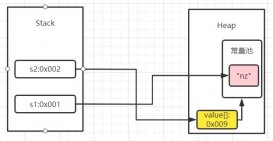
一.經典快排思想
前提條件:給定一個無序數組arr
- 取這個數組最后一個數 num 作為標準,將前面部分的數分為兩部分,使得<=num的部分在左邊,>num的數在右邊;
- 然后將最后一個數和>num部分的第一個數進行交換,就使得原本在數組最后位置的num找到了正確的位置,它的左邊都是比它小的以及和它一樣的數,右邊都是比它大的數
- 回到1,進行遞歸或迭代,使得所有的數都找到正確的位
二.通過荷蘭國旗問題改進快排
什么是荷蘭國旗問題?
已知一個整形數組arr,和一個整數num,請把小于num的數放在數組的左邊,等于num的數放在數組的中間,大于num的數放在數組的右邊。
解決思路:
遍歷數組
- 1. 若比num小,當前位置和小于的最后一個位置+1的值交換,并當前位置++;
- 2. 若比num大,當前位置和大于的第一個位置-1的值交換;
- 3. 若等于num的值,當前位置++;
附上代碼:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
public static void netherlandsflag(int[] arr, int l, int r, int num) { int i = l; int p1 = l-1; int p2 = r+1; //終止條件:當前數的位置在大于區的前一個 while(i < p2) { if(arr[i] < num) { //當前數比num小,放左邊,i位置上的數和l上的數進行交換,并且i++,l++ swap(arr, i++, ++p1); } else if(arr[i] == num) { //當前數和num相等,i++ i++; } else { //當前數比num大,放右邊,i位置上的數和r上的數進行交換,并且i++,r-- swap(arr, i, --p2); } }} |
我們可以發現,荷蘭國旗問題和經典快排不同的就只是將<=num改為了< num和=num兩部分,借用這個思想使得原來每次只可以讓一個數找到正確的位置改進為了每次至少讓一個數找到位置。
三.在這基礎上將其改為隨機快排
隨機快排改進的地方只是在選取數的時候,將每次都選取最后位置的數改為選取隨機的一個數作為num,這樣做的好處是什么呢?
1.選取最后一個數:如果是一個已經排好序的數組,每次找到位置之后,左邊是要進行排序的部分,數組長度是原長度-1,它的時間復雜度就是o(n^2);如果每次找到的數都是中間的位置,它的時間復雜度就只有o(logn)
2.然而以隨機數作為選取的標準num的時候,因為是隨機的,就只能通過數學期望去計算它的時間復雜度,時間復雜度是o(logn)
下面附上最終的快排代碼及注釋
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
/* * swap(int[] arr, int i, int j);是將arr數組的i和j位置上的數交換的方法 */public static void quicksort(int[] arr) { // 如果為空或長度為1不需要排序,直接返回 if(arr == null || arr.length < 2) return; else quicksort(arr, 0, arr.length - 1);}// 遞歸排序public static void quicksort(int[] arr, int l, int r) { if(l < r) { /* * 隨機快排的隨機就在這 * 是隨機選取了一個數,和 r 進行了交換,然后使用這個數作為num, * 所以每次選取的num是隨機的, * 在計算時間復雜度時,是沒有最優最差情況的 * 而是通過一個長期的數學期望計算的,結果是o(n*logn) */ swap(arr, l + (int) (math.random() * (r - l + 1)), r); int[] border = partition(arr, l, r); // 小于區和大于區進行遞歸 quicksort(arr, l, border[0] - 1); quicksort(arr, border[1] + 1, r); }}// 將給定數組劃分為小于區、等于區和大于區public static int[] partition(int[] arr, int l, int r) { int num = arr[r]; int less = l - 1; int more = r + 1; int curr = l; // 分為小于區等于區和大于區 while(curr < more) { if(arr[curr] < num) { swap(arr, curr++, ++less); } else if(arr[curr] > num) { swap(arr, curr, --more); } else { curr++; } } //返回等于區的左右邊界的下標,通過下標確定小于區和大于區遞歸時的參數 return new int[] {less + 1, more - 1};} |
總結
以上就是這篇文章的全部內容了,希望本文的內容對大家的學習或者工作具有一定的參考學習價值,謝謝大家對服務器之家的支持。如果你想了解更多相關內容請查看下面相關鏈接
原文鏈接:https://blog.csdn.net/sdr_zd/article/details/79425077