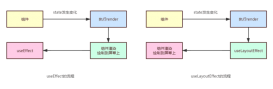
React中Diff算法又稱為調和算法,對應函數名為reconcileChildren,它的主要作用是標記更新過程中那些元素發生了變化,這些變化包括新增、移動、刪除。過程發生在beginWork階段,只有非初次渲染才會Diff。
以前看過一些文章將Diff算法表述為兩顆Fiber樹的比較,這是不正確的,實際的Diff過程是一組現有的Fiber節點和新的由JSX生成的ReactElement的比較,然后生成新的Fiber節點的過程,這個過程中也會嘗試復用現有Fiber節點。
節點Diff又分為兩種:
-
單節點Diff ——
Element、Portal、string、number。 -
多節點Diff ——
Array、Iterator。
以下React版本為17.0.1,代碼文件為ReactChildFiber.old.js。
單節點Diff
單節點Diff比較簡單,只有key相同并且type相同的情況才會嘗試復用節點,否則會返回新的節點。
單節點大部分情況下我們都不會去賦值key,所以它們默認為null,也是相同的。
reconcileSingleElement
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
// 單節點比較function reconcileSingleElement( returnFiber: Fiber, currentFirstChild: Fiber | null, element: ReactElement, lanes: Lanes,): Fiber { // 當前新的reactElement的key const key = element.key; // 當前的child fiber節點 let child = currentFirstChild; while (child !== null) { // key相同的情況才diff if (child.key === key) { switch (child.tag) { // ... default: { // 當前fiber和reactElement的type相同時 if (child.elementType === element.type) { // 刪除同級的其他節點 deleteRemainingChildren(returnFiber, child.sibling); // 復用當前child fiber const existing = useFiber(child, element.props); existing.ref = coerceRef(returnFiber, child, element); existing.return = returnFiber; // 返回可復用的child fiber return existing; } break; } } // 不匹配刪除節點 deleteRemainingChildren(returnFiber, child); break; } else { // key不同直接刪除節點 deleteChild(returnFiber, child); } child = child.sibling; } // 新的Fiber節點 const created = createFiberFromElement(element, returnFiber.mode, lanes); created.ref = coerceRef(returnFiber, currentFirstChild, element); created.return = returnFiber; return created;} |
多節點Diff
源碼中將多節點分為了數組節點和可迭代節點。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
if (isArray(newChild)) { return reconcileChildrenArray( returnFiber, currentFirstChild, newChild, lanes, );}if (getIteratorFn(newChild)) { return reconcileChildrenIterator( returnFiber, currentFirstChild, newChild, lanes, );} |
對應的Diff函數分別是reconcileChildrenArray和reconcileChildrenIterator。它們的核心Diff邏輯是相同的,所以只分析數組節點的Diff —— reconcileChildrenArray函數。
這一段的代碼比較長,但邏輯很清晰,從分割線分為兩輪遍歷。
- 第一輪遍歷的是順序相同且key也相同的節點,這些節點需要做更新操作。
- 第二輪遍歷的是順序不同,可能key也不同的節點,這些節點需要做新增、移動或刪除操作。
第一輪遍歷只針對key和順序都相同的情況,這些key對應的節點位置沒有發生改變,只需要做更新操作,一旦遍歷遇到key不同的情況就需要跳出循環。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
// 舊節點<li key="0"/><li key="1"/><li key="2"/>// 新節點<li key="0"/><li key="1"/><li key="5"/>// key="5"不同,跳出遍歷// 第一輪遍歷的節點<li key="0"/><li key="1"/>// <li key="2"/>和<li key="5"/>留在第二輪遍歷比較。 |
在第一輪遍歷完后也分為兩種情況。
- 新節點數量少于舊節點數量,這時候需要把多余的舊節點標記為刪除。
- 新節點數量大于舊節點數量,這時候需要把多余的新節點標記為新增。
第二輪遍歷針對key不同或順序不同的情況,可能情況如下:
|
1
2
3
4
5
6
7
8
9
10
|
// 舊節點<li key="0"/><li key="1"/><li key="2"/>// 新節點<li key="0"/><li key="2"/><li key="1"/>// 第二輪遍歷對比<li key="2"/>、<li key="1"/>這兩個節點 |
第二輪的遍歷會稍微復雜一點,后文在細講。
詳細的代碼如下。
reconcileChildrenArray
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
|
function reconcileChildrenArray( returnFiber: Fiber, currentFirstChild: Fiber | null, newChildren: Array<*>, lanes: Lanes,): Fiber | null { // 函數返回的Fiber節點 let resultingFirstChild: Fiber | null = null; let previousNewFiber: Fiber | null = null; // oldFiber為鏈表 let oldFiber = currentFirstChild; // 用來判斷節點是否移動 let lastPlacedIndex = 0; let newIdx = 0; let nextOldFiber = null; // 第一輪遍歷,只遍歷key相同的節點 for (; oldFiber !== null && newIdx < newChildren.length; newIdx++) { if (oldFiber.index > newIdx) { nextOldFiber = oldFiber; oldFiber = null; } else { // 每次循環舊的fiber節點都會指向兄弟元素也就是下次循環的fiber節點 nextOldFiber = oldFiber.sibling; } // key相同返回fiber節點,key不同返回null // 如果type相同復用節點,不同返回新節點 const newFiber = updateSlot( returnFiber, oldFiber, newChildren[newIdx], lanes, ); // newFiber為null表示key不同,跳出循環 if (newFiber === null) { if (oldFiber === null) { oldFiber = nextOldFiber; } break; } // newFiber.alternate為null就是新節點,說明type不同創建了新fiber節點 if (oldFiber && newFiber.alternate === null) { // 需要把oldFiber標記刪除 deleteChild(returnFiber, oldFiber); } // 放置節點,更新lastPlacedIndex lastPlacedIndex = placeChild(newFiber, lastPlacedIndex, newIdx); // 組成新fiber節點鏈 if (previousNewFiber === null) { resultingFirstChild = newFiber; } else { previousNewFiber.sibling = newFiber; } previousNewFiber = newFiber; oldFiber = nextOldFiber; } /* 第一輪遍歷完后新節點數量少于舊節點數量 newChildren已經遍歷完,刪除掉剩下的fiber節點,可能情況如下 ?? 以前 <li key="0"/> <li key="1"/> <li key="2"/> 新的 <li key="0"/> <li key="1"/> 就會把<li key="2"/>刪除 */ if (newIdx === newChildren.length) { deleteRemainingChildren(returnFiber, oldFiber); return resultingFirstChild; } /* 第一輪遍歷完新節點數量大于舊節點數量 oldFiber已經遍歷完,可能情況如下 ?? 以前 <li key="0"/> <li key="1"/> 新的 <li key="0"/> <li key="1"/> <li key="2"/> 就會添加新的<li key="2"/>,這一段是新節點的插入邏輯 */ if (oldFiber === null) { for (; newIdx < newChildren.length; newIdx++) { const newFiber = createChild(returnFiber, newChildren[newIdx], lanes); if (newFiber === null) { continue; } lastPlacedIndex = placeChild(newFiber, lastPlacedIndex, newIdx); // 組成新fiber節點鏈 if (previousNewFiber === null) { resultingFirstChild = newFiber; } else { previousNewFiber.sibling = newFiber; } previousNewFiber = newFiber; } return resultingFirstChild; } // --------------------------------------------------------------------- // 用剩余的oldFiber創建一個key->fiber節點的Map,方便用key來獲取對應的舊fiber節點 const existingChildren = mapRemainingChildren(returnFiber, oldFiber); // 第二輪遍歷,繼續遍歷剩余的節點,這些節點可能是需要移動或者刪除的 for (; newIdx < newChildren.length; newIdx++) { // 從map中獲取對應對應key的舊節點,返回更新后的新節點 const newFiber = updateFromMap( existingChildren, returnFiber, newIdx, newChildren[newIdx], lanes, ); if (newFiber !== null) { // 復用的新節點,從map里刪除老的節點,對應的情況可能是位置的改變 if (newFiber.alternate !== null) { // 復用的節點要移除map,因為map里剩余的節點都會被標記Deletion刪除 existingChildren.delete( newFiber.key === null ? newIdx : newFiber.key, ); } // 放置節點同時節點判斷是否移動 lastPlacedIndex = placeChild(newFiber, lastPlacedIndex, newIdx); if (previousNewFiber === null) { resultingFirstChild = newFiber; } else { previousNewFiber.sibling = newFiber; } previousNewFiber = newFiber; } } // 刪除剩下的無用節點 existingChildren.forEach(child => deleteChild(returnFiber, child)); return resultingFirstChild;} |
第一輪遍歷比較好理解,這里再細分析一下第二輪遍歷,因為第二輪會出現復用是否需要移動的問題。
第二輪遍歷首先遍歷剩余的oldFiber,組成一個key -> 舊fiber節點的Map,這用可以通過key來快速的獲取舊節點。
接下來的遍歷依然是使用的新節點為遍歷對象,每次遍歷使用新節點的key從Map中取出舊節點來對比是否能復用,對應的函數為updateFromMap。
如果節點存在alternate屬性,則是復用的節點,這時候需要將它從existingChildren里移除,后續會把第二輪遍歷完后依然存在在existingChildren里的節點標記為刪除。
如何判斷節點移動了?
這里存在一個變量lastPlacedIndex用來判斷節點是否移動,每次將節點添加到新的Fiber鏈表中,都會更新這個值。
當復用的節點oldIndex小于lastPlacedIndex時,則為移動,如果不需要移動,則會將lastPlacedIndex更新為較大的oldIndex,下一個節點會以新值判斷,代碼如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
function placeChild( newFiber: Fiber, lastPlacedIndex: number, newIndex: number,): number { newFiber.index = newIndex; const current = newFiber.alternate; if (current !== null) { const oldIndex = current.index; if (oldIndex < lastPlacedIndex) { // 節點移動 newFiber.flags = Placement; return lastPlacedIndex; } else { // 節點位置無變化 return oldIndex; } } else { // 插入的新節點 newFiber.flags = Placement; return lastPlacedIndex; }} |
舉個例子:
|
1
2
3
4
|
// 舊abcd// 新acbd |
abcd均為key值。
第一輪遍歷后剩下的需要對比節點:
|
1
2
3
4
|
// 舊bcd// 新cbd |
a節點在第一輪已經復用,并且調用過placeChild,這時lastPlacedIndex值為0。
進入第二輪遍歷,依然是以新節點為遍歷對象。
|
1
2
3
|
c => 在舊節點中存在,可復用,它的index在舊節點中為2,2 > lastPlacedIndex(0),不需要移動,將lastPlacedIndex賦值為2。b => 在舊節點中存在,可復用,它的index在舊節點中為1,1 < lastPlacedIndex(2),需要移動,標記Placement。d => 在舊節點中存在,可復用,它的index在舊節點中為3,3 > lastPlacedIndex(2),不需要移動。 |
由這個例子可以看出,React中將右側不需要移動的節點作為參照,將需要移動的節點都是統一從左向右移動的。
在后續Layout階段會將這里標記了Placement的節點做insertBefore操作。
總結
React中的Diff算法核心代碼不算很長,但是卻引入key巧妙的將復雜度由O(n3 )變為了O(n)。
碼農內卷太嚴重,所以不得不學習源碼了。
以上就是react diff算法源碼解析的詳細內容,更多關于react diff算法的資料請關注服務器之家其它相關文章!
原文鏈接:https://juejin.cn/post/6949092569275957256