逆轉交替合并兩個鏈表，即從一個鏈表的尾指針指向另一個鏈表的尾指針，依次逆轉交替進行合并。下面就通過實例來詳細的介紹該逆轉交替合并兩個鏈表的思路與實現代碼。

一、問題描述

鏈表A和B
A: 1->2->3->4
B: a->b->c->d
請逆轉交替合并兩個鏈表，示例結果如下：
4->d->3->c->2->b->1->a
節點類型定義如下:

二、源代碼：

傳入兩個A和B鏈表，返回處理后的鏈表：

三、解析：

程序分成三個部分——while循環之前、while循環體、while循環之后。
1）處理之前的鏈表A和B

2）while循環——核心的處理部分
這里處理程序的可重復的部分，我們的目標是紅色的部分，要達成紅色的鏈接模式，有兩個原子結構：深紅色圓圈1和藍色圓圈2

但是1中需要特別處理a所在的節點，僅對于a所在的節點需要一個next=null的操作，也就是說1中的第一個原子要放在循環之外實現，這包括1指向a，b指向1的操作。

換種方式，如果使用2方式，就只需要將1指向a放在循環之外。所以，這里采用了2中描述的原子結構。

原子結構需要的信息

當我們進行到某一次循環時，假設進行到藍色圓圈的操作了，這時候我們鏈表的狀態為：

更為直觀的畫法為：

它涉及到3個節點——2,3和c。其中紅色部分是我們希望做到的鏈接方式。為了鏈接c->2,3->c，必須知道有相應的指針記錄他們的位置。所以在循環之前我們需要掌握這三個元素的地址，并且在處理完之后，用相同的方式表示下一次需要處理的原子結構。

例如以下這種方式記錄這次循環中設計的3個節點的地址：

A、nA、B代表指向相應節點的指針或者說是引用。

在處理完成之后需要用相同的方式記錄下一次原子結構涉及的節點，這樣才能保證循環能夠按統一邏輯執行下去，我們的目標是：

這些賦值操作正是循環體的中代碼所做的事情，恰好代碼也是按照上面指定的命名形式，有一點區別，圖中的nA代表代碼中的nextA。除此之外，代碼中定義了nextB作為一個中間變量，用來記錄c->d斷開之前d節點的地址，因為c指向2之后就會失去對d的聯系，這個中間變量是必須的。

3）while循環之前——解決預備操作所帶來的問題

我們還沒有處理a節點，因為它太特殊了，沒有合適的原子結構能包括它。所以我們把它放在循環體之外，并且為循環做好準備工作，我們希望的結果是這樣：

在這之后我們就可以把1，2，b放在循環體中處理。這里也考慮了A、B都只有一個節點的情況，也需要單獨處理。

4）while循環之后——最后的處理

當我們發現B鏈表到達末尾時，結束循環。但這時候并有處理末尾節點，換句話說，末尾節點不在原子結構中。我們的循環會停止在這個原子結構中：

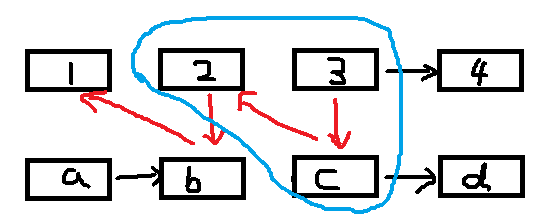
作為最后的操作，我們需要手動處理d->3,4->d的鏈接步驟——這也是沒有辦法的，因為原子結構的處理必須找到能夠把所有指針傳遞下去的節點，作為最后的節點是沒辦法吧指針繼續傳遞下去。

這不是一個完整的方法，還有很多事情沒有處理，比如輸入的A、B如果不等長，應該如何處理。另外Node數據結構并沒有完整的定義，不過這都不是本文討論的重點。

通過以上詳細的解析，希望能夠幫助大家很好的理解該逆轉交替合并兩個鏈表的方法與實現。