一、二叉排序樹定義
1.二叉排序樹的定義
二叉排序樹(Binary Sort Tree)又稱二叉查找(搜索)樹(Binary Search Tree)。其定義為:二叉排序樹或者是空樹,或者是滿足如下性質(zhì)的二叉樹:
①若它的左子樹非空,則左子樹上所有結(jié)點的值均小于根結(jié)點的值;
②若它的右子樹非空,則右子樹上所有結(jié)點的值均大于根結(jié)點的值;
③左、右子樹本身又各是一棵二叉排序樹。
上述性質(zhì)簡稱二叉排序樹性質(zhì)(BST性質(zhì)),故二叉排序樹實際上是滿足BST性質(zhì)的二叉樹。

2.二叉排序樹的性質(zhì)
按中序遍歷二叉排序樹,所得到的中序遍歷序列是一個遞增有序序列。
3.二叉排序樹的插入
在二叉排序樹中插入新結(jié)點,要保證插入后的二叉樹仍符合二叉排序樹的定義。
插入過程:
若二叉排序樹為空,則待插入結(jié)點*S作為根結(jié)點插入到空樹中;
當(dāng)非空時,將待插結(jié)點關(guān)鍵字S->key和樹根關(guān)鍵字t->key進行比較,若s->key = t->key,則無須插入,若s->key< t->key,則插入到根的左子樹中,若s->key> t->key,則插入到根的右子樹中。而子樹中的插入過程和在樹中的插入過程相同,如此進行下去,直到把結(jié)點*s作為一個新的樹葉插入到二叉排序樹中,或者直到發(fā)現(xiàn)樹已有相同關(guān)鍵字的結(jié)點為止。
4.二叉排序樹的查找
假定二叉排序樹的根結(jié)點指針為 root ,給定的關(guān)鍵字值為 K ,則查找算法可描述為:
① 置初值: q = root ;
② 如果 K = q -> key ,則查找成功,算法結(jié)束;
③ 否則,如果 K < q -> key ,而且 q 的左子樹非空,則將 q 的左子樹根送 q ,轉(zhuǎn)步驟②;否則,查找失敗,結(jié)束算法;
④ 否則,如果 K > q -> key ,而且 q 的右子樹非空,則將 q 的右子樹根送 q ,轉(zhuǎn)步驟②;否則,查找失敗,算法結(jié)束。
5.二叉排序樹的刪除
假設(shè)被刪結(jié)點是*p,其雙親是*f,不失一般性,設(shè)*p是*f的左孩子,下面分三種情況討論:
⑴ 若結(jié)點*p是葉子結(jié)點,則只需修改其雙親結(jié)點*f的指針即可。
⑵ 若結(jié)點*p只有左子樹PL或者只有右子樹PR,則只要使PL或PR 成為其雙親結(jié)點的左子樹即可。
⑶ 若結(jié)點*p的左、右子樹均非空,先找到*p的中序前趨(或后繼)結(jié)點*s(注意*s是*p的左子樹中的最右下的結(jié)點,它的右鏈域為空),然后有兩種做法:① 令*p的左子樹直接鏈到*p的雙親結(jié)點*f的左鏈上,而*p的右子樹鏈到*p的中序前趨結(jié)點*s的右鏈上。② 以*p的中序前趨結(jié)點*s代替*p(即把*s的數(shù)據(jù)復(fù)制到*p中),將*s的左子樹鏈到*s的雙親結(jié)點*q的左(或右)鏈上。
6、二叉樹的遍歷
二叉樹的遍歷有三種方式,如下:
(1)前序遍歷(DLR),首先訪問根結(jié)點,然后遍歷左子樹,最后遍歷右子樹。簡記根-左-右。
(2)中序遍歷(LDR),首先遍歷左子樹,然后訪問根結(jié)點,最后遍歷右子樹。簡記左-根-右。
(3)后序遍歷(LRD),首先遍歷左子樹,然后遍歷右子樹,最后訪問根結(jié)點。簡記左-右-根。
二、代碼編寫
1、樹節(jié)點類的定義0
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
package com.lin; /** * 功能概要: */public class TreeNode { public Integer data; /*該節(jié)點的父節(jié)點*/ public TreeNode parent; /*該節(jié)點的左子節(jié)點*/ public TreeNode left; /*該節(jié)點的右子節(jié)點*/ public TreeNode right; public TreeNode(Integer data) { this.data = data; } @Override public String toString() { return "TreeNode [data=" + data + "]"; } } |
2、二叉排序樹的定義
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
|
package com.lin; /** * 功能概要:排序/平衡二叉樹 */public class SearchTree { public TreeNode root; public long size; /** * 往樹中加節(jié)點 * @param data * @return Boolean 插入成功返回true */ public Boolean addTreeNode(Integer data) { if (null == root) { root = new TreeNode(data); System.out.println("數(shù)據(jù)成功插入到平衡二叉樹中"); return true; } TreeNode treeNode = new TreeNode(data);// 即將被插入的數(shù)據(jù) TreeNode currentNode = root; TreeNode parentNode; while (true) { parentNode = currentNode;// 保存父節(jié)點 // 插入的數(shù)據(jù)比父節(jié)點小 if (currentNode.data > data) { currentNode = currentNode.left; // 當(dāng)前父節(jié)點的左子節(jié)點為空 if (null == currentNode) { parentNode.left = treeNode; treeNode.parent = parentNode; System.out.println("數(shù)據(jù)成功插入到二叉查找樹中"); size++; return true; } // 插入的數(shù)據(jù)比父節(jié)點大 } else if (currentNode.data < data) { currentNode = currentNode.right; // 當(dāng)前父節(jié)點的右子節(jié)點為空 if (null == currentNode) { parentNode.right = treeNode; treeNode.parent = parentNode; System.out.println("數(shù)據(jù)成功插入到二叉查找樹中"); size++; return true; } } else { System.out.println("輸入數(shù)據(jù)與節(jié)點的數(shù)據(jù)相同"); return false; } } } /** * @param data * @return TreeNode */ public TreeNode findTreeNode(Integer data){ if(null == root){ return null; } TreeNode current = root; while(current != null){ if(current.data > data){ current = current.left; }else if(current.data < data){ current = current.right; }else { return current; } } return null; } } |
這里暫時只放了一個增加和查找的方法
3、前、中、后遍歷
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
|
package com.lin; import java.util.Stack; /** * 功能概要: */public class TreeOrder { /** * 遞歸實現(xiàn)前序遍歷 * @author linbingwen * @since 2015年8月29日 * @param treeNode */ public static void preOrderMethodOne(TreeNode treeNode) { if (null != treeNode) { System.out.print(treeNode.data + " "); if (null != treeNode.left) { preOrderMethodOne(treeNode.left); } if (null != treeNode.right) { preOrderMethodOne(treeNode.right); } } } /** * 循環(huán)實現(xiàn)前序遍歷 * @param treeNode */ public static void preOrderMethodTwo(TreeNode treeNode) { if (null != treeNode) { Stack<TreeNode> stack = new Stack<TreeNode>(); stack.push(treeNode); while (!stack.isEmpty()) { TreeNode tempNode = stack.pop(); System.out.print(tempNode.data + " "); // 右子節(jié)點不為null,先把右子節(jié)點放進去 if (null != tempNode.right) { stack.push(tempNode.right); } // 放完右子節(jié)點放左子節(jié)點,下次先取 if (null != tempNode.left) { stack.push(tempNode.left); } } } } /** * 遞歸實現(xiàn)中序遍歷 * @param treeNode */ public static void medOrderMethodOne(TreeNode treeNode){ if (null != treeNode) { if (null != treeNode.left) { medOrderMethodOne(treeNode.left); } System.out.print(treeNode.data + " "); if (null != treeNode.right) { medOrderMethodOne(treeNode.right); } } } /** * 循環(huán)實現(xiàn)中序遍歷 * @param treeNode */ public static void medOrderMethodTwo(TreeNode treeNode){ Stack<TreeNode> stack = new Stack<TreeNode>(); TreeNode current = treeNode; while (current != null || !stack.isEmpty()) { while(current != null) { stack.push(current); current = current.left; } if (!stack.isEmpty()) { current = stack.pop(); System.out.print(current.data+" "); current = current.right; } } } /** * 遞歸實現(xiàn)后序遍歷 * @param treeNode */ public static void postOrderMethodOne(TreeNode treeNode){ if (null != treeNode) { if (null != treeNode.left) { postOrderMethodOne(treeNode.left); } if (null != treeNode.right) { postOrderMethodOne(treeNode.right); } System.out.print(treeNode.data + " "); } } /** * 循環(huán)實現(xiàn)后序遍歷 * @param treeNode */ public static void postOrderMethodTwo(TreeNode treeNode){ if (null != treeNode) { Stack<TreeNode> stack = new Stack<TreeNode>(); TreeNode current = treeNode; TreeNode rightNode = null; while(current != null || !stack.isEmpty()) { while(current != null) { stack.push(current); current = current.left; } current = stack.pop(); while (current != null && (current.right == null ||current.right == rightNode)) { System.out.print(current.data + " "); rightNode = current; if (stack.isEmpty()){ System.out.println(); return; } current = stack.pop(); } stack.push(current); current = current.right; } } } } |
4、使用方法
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
package com.lin; /** * 功能概要: */public class SearchTreeTest { /** * @param args */ public static void main(String[] args) { SearchTree tree = new SearchTree(); tree.addTreeNode(50); tree.addTreeNode(80); tree.addTreeNode(20); tree.addTreeNode(60); tree.addTreeNode(10); tree.addTreeNode(30); tree.addTreeNode(70); tree.addTreeNode(90); tree.addTreeNode(100); tree.addTreeNode(40); System.out.println("=============================="+"采用遞歸的前序遍歷開始"+"=============================="); TreeOrder.preOrderMethodOne(tree.root); System.out.println(); System.out.println("=============================="+"采用循環(huán)的前序遍歷開始"+"=============================="); TreeOrder.preOrderMethodTwo(tree.root); System.out.println(); System.out.println("=============================="+"采用遞歸的后序遍歷開始"+"=============================="); TreeOrder.postOrderMethodOne(tree.root); System.out.println(); System.out.println("=============================="+"采用循環(huán)的后序遍歷開始"+"=============================="); TreeOrder.postOrderMethodTwo(tree.root); System.out.println(); System.out.println("=============================="+"采用遞歸的中序遍歷開始"+"=============================="); TreeOrder.medOrderMethodOne(tree.root); System.out.println(); System.out.println("=============================="+"采用循環(huán)的中序遍歷開始"+"=============================="); TreeOrder.medOrderMethodTwo(tree.root); } } |
輸出結(jié)果:

同樣,進行查找過程如下:
|
1
2
|
TreeNode node = tree.findTreeNode(100); System.out.println(node); |
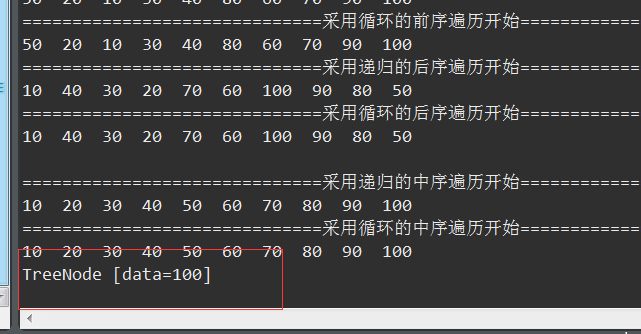
結(jié)果是正確的
以上就是關(guān)于Java二叉排序樹的詳細(xì)介紹,希望對大家的學(xué)習(xí)java程序設(shè)計有所幫助。













