快速排序是C.R.A.Hoare于1962年提出的一種劃分交換排序。該方法的基本思想是:
1.先從數(shù)列中取出一個(gè)數(shù)作為基準(zhǔn)數(shù)。
2.分區(qū)過程,將比這個(gè)數(shù)大的數(shù)全放到它的右邊,小于或等于它的數(shù)全放到它的左邊。
3.再對(duì)左右區(qū)間重復(fù)第二步,直到各區(qū)間只有一個(gè)數(shù)。
算法的思路很清晰,但是如果在區(qū)間劃分過程中邊界值沒有處理好,也是很容易出現(xiàn)bug的。下面給出兩種比較清晰的思維來指導(dǎo)區(qū)間劃分代碼的編寫。
第一種思維即所謂的挖坑法思維,下面通過分析一個(gè)實(shí)例來分析一下挖坑法的過程:
以一個(gè)數(shù)組作為示例,取區(qū)間第一個(gè)數(shù)為基準(zhǔn)數(shù)。

初始時(shí),left = 0; right= 9; X = a[left] = 72
由于已經(jīng)將a[0]中的數(shù)保存到X中,可以理解成在數(shù)組a[0]上挖了個(gè)坑,可以將其它數(shù)據(jù)填充到這來。
從right開始向前找一個(gè)<=X的數(shù)。顯然,right=8時(shí),符合條件,將a[8]挖出再填到上一個(gè)坑a[left]中。 這樣一個(gè)坑a[0]就被搞定了,但又形成了一個(gè)新坑a[8],這怎么辦了?簡單,再找數(shù)字來填a[8]這個(gè)坑。這次從left開始向后找一個(gè)大于X的數(shù),當(dāng)left=3,符合條件,將a[3]挖出再填到上一個(gè)坑a[right] 中;
數(shù)組變?yōu)椋?/p>

再重復(fù)上面的步驟,最終數(shù)組將變成如下形式:
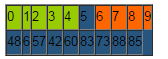
可以看出a[5]前面的數(shù)字都小于它,a[5]后面的數(shù)字都大于它。將X填入a[5]的坑中,數(shù)據(jù)變?yōu)椋?br />

因此再對(duì)a[0…4]和a[6…9]這二個(gè)子區(qū)間重復(fù)上述步驟就可以了。
對(duì)挖坑填數(shù)進(jìn)行總結(jié)
1.i =L; j = R; 將基準(zhǔn)數(shù)挖出形成第一個(gè)坑a[i]。
2.j--由后向前找比它小的數(shù),找到后挖出此數(shù)填前一個(gè)坑a[i]中。
3.i++由前向后找比它大的數(shù),找到后也挖出此數(shù)填到前一個(gè)坑a[j]中。
4.再重復(fù)執(zhí)行2,3二步,直到i==j,將基準(zhǔn)數(shù)填入a[i]中。
照此分區(qū)方法,快速排序Java代碼如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
public class Partition { /** * 基于base劃分,小的在左,大的在右, 不要求整個(gè)序列有序 * * @param ary * @param base */ static void sort(int[] ary, int base) { int left = 0; int right = ary.length - 1; int leftpoint = left, rightpoint = right; while (true) { // 分成左右兩邊同時(shí)進(jìn)行比較,一邊從左向右,一邊從右向左, while (leftpoint < right && ary[leftpoint++] < base); //leftpoint大于right或ary[leftpoint]>base停止循環(huán) while (rightpoint >= left && ary[rightpoint--] > base); //反之 System.out.println("左邊需要交換的索引:" + (leftpoint-1)); System.out.println("右邊需要交換的索引:"+ (rightpoint+1)); //上面拿到了不符合條件的兩個(gè)索引,即需要交換的兩個(gè)索引 if (leftpoint - 1 < rightpoint + 1) {//需要交換 swap(ary, leftpoint - 1, rightpoint + 1); Util.printArray(ary); leftpoint = left; rightpoint = right; } else { break; } } } private static void swap(int[] ary, int a, int b) { int temp = ary[a]; ary[a] = ary[b]; ary[b] = temp; } public static void main(String[] args) { int[] ary = Util.generateIntArray(10); System.out.println("原序列:"); Util.printArray(ary); sort(ary, 5); System.out.println("排序后:"); Util.printArray(ary); } } |
結(jié)果:
|
1
2
3
4
5
6
7
8
9
10
11
12
|
原序列: [2, 8, 4, 3, 7, 5, 1, 9, 0, 6] 左邊需要交換的索引:1 右邊需要交換的索引:8 [2, 0, 4, 3, 7, 5, 1, 9, 8, 6] 左邊需要交換的索引:4 右邊需要交換的索引:6 [2, 0, 4, 3, 1, 5, 7, 9, 8, 6] 左邊需要交換的索引:5 右邊需要交換的索引:5 排序后: [2, 0, 4, 3, 1, 5, 7, 9, 8, 6] |
區(qū)間劃分的的另一種指導(dǎo)思維:
將數(shù)組的第一個(gè)元素作為區(qū)間劃分值,從第二個(gè)元素開始分區(qū),直到形成如圖所示的結(jié)果,

然后交換l<t區(qū)間的右邊界值和t,形成如下的結(jié)果:

如此,可以如下編寫快速排序代碼:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
public void qSort(int array[],int left,int right) { if(left < right){ int key = array[left]; int high = right; int low = left+1; while(true){ while(low <= high && array[low] <= key) low++; while(low <= high && array[high] >= key) high--; if(low > high) break; swap(array,low,high); } swap(array,left,high); printArray(array); qSort(array,left,high-1); qSort(array,high+1,right); } } |