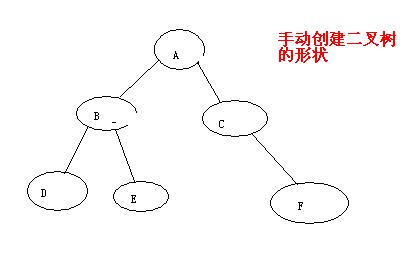
二叉樹的分類(按存儲結構)
樹的分類(按存儲結構)
順序存儲(用數組表示(靜態二叉樹))
鏈式存儲
一些特別的二叉根:
完全二叉樹,平衡二叉樹(AVL),線索二叉樹,三叉的(帶父親的指針)
二叉搜索樹或者叫二叉 查找樹(BST)
所用二叉樹如下圖所示:
二叉樹的Java實現(鏈式存儲結構)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
|
class TreeNode { private int key = 0; private String data = null; private boolean isVisted = false; private TreeNode leftChild = null; private TreeNode rightChild = null; public TreeNode(){ } public TreeNode(int key, String data){ this.key = key; this.data = data; this.leftChild = null; this.rightChild = null; } public int getKey() { return key; } public void setKey(int key) { this.key = key; } public String getData() { return data; } public void setData(String data) { this.data = data; } public TreeNode getLeftChild() { return leftChild; } public void setLeftChild(TreeNode leftChild) { this.leftChild = leftChild; } public TreeNode getRightChild() { return rightChild; } public void setRightChild(TreeNode rightChild) { this.rightChild = rightChild; } public boolean isVisted() { return isVisted; } public void setVisted(boolean isVisted) { this.isVisted = isVisted; }}public class BinaryTree { private TreeNode root = null; public BinaryTree() { root = new TreeNode(1, "rootNode(A)"); } public void createBinTree(TreeNode root){ //手動的創建(結構如圖所示) TreeNode newNodeB = new TreeNode(2,"B"); TreeNode newNodeC = new TreeNode(3,"C"); TreeNode newNodeD = new TreeNode(4,"D"); TreeNode newNodeE = new TreeNode(5,"E"); TreeNode newNodeF = new TreeNode(6,"F"); root.setLeftChild(newNodeB); root.setRightChild(newNodeC); root.getLeftChild().setLeftChild(newNodeD); root.getLeftChild().setRightChild(newNodeE); root.getRightChild().setRightChild(newNodeF); } public boolean IsEmpty() { // 判二叉樹空否 return root == null; } public int Height() { // 求樹高度 return Height(root); } public int Height(TreeNode subTree) { if (subTree == null) return 0; //遞歸結束:空樹高度為0 else { int i = Height(subTree.getLeftChild()); int j = Height(subTree.getRightChild()); return (i < j) ? j + 1 : i + 1; } } public int Size() { // 求結點數 return Size(root); } public int Size(TreeNode subTree) { if (subTree == null) return 0; else { return 1 + Size(subTree.getLeftChild()) + Size(subTree.getRightChild()); } } public TreeNode Parent(TreeNode element) { //返回雙親結點 return (root == null || root == element) ? null : Parent(root, element); } public TreeNode Parent(TreeNode subTree, TreeNode element) { if (subTree == null) return null; if (subTree.getLeftChild() == element || subTree.getRightChild() == element) //找到, 返回父結點地址 return subTree; TreeNode p; //先在左子樹中找,如果左子樹中沒有找到,才到右子樹去找 if ((p = Parent(subTree.getLeftChild(), element)) != null) //遞歸在左子樹中搜索 return p; else //遞歸在左子樹中搜索 return Parent(subTree.getRightChild(), element); } public TreeNode LeftChild(TreeNode element) { //返回左子樹 return (element != null) ? element.getLeftChild() : null; } public TreeNode RightChild(TreeNode element) { //返回右子樹 return (element != null) ? element.getRightChild() : null; } public TreeNode getRoot() { //取得根結點 return root; } public void destroy(TreeNode subTree) { //私有函數: 刪除根為subTree的子樹 if (subTree != null) { destroy(subTree.getLeftChild()); //刪除左子樹 destroy(subTree.getRightChild()); //刪除右子樹 //delete subTree; //刪除根結點 subTree = null; } } public void Traverse(TreeNode subTree) { System.out.println("key:" + subTree.getKey() + "--name:" + subTree.getData()); Traverse(subTree.getLeftChild()); Traverse(subTree.getRightChild()); } public void PreOrder(TreeNode subTree) { //先根 if (subTree != null) { visted(subTree); PreOrder(subTree.getLeftChild()); PreOrder(subTree.getRightChild()); } } public void InOrder(TreeNode subTree) { //中根 if (subTree != null) { InOrder(subTree.getLeftChild()); visted(subTree); InOrder(subTree.getRightChild()); } } public void PostOrder(TreeNode subTree) { //后根 if (subTree != null) { PostOrder(subTree.getLeftChild()); PostOrder(subTree.getRightChild()); visted(subTree); } } public void LevelOrder(TreeNode subTree) { //水平遍邊 } public boolean Insert(TreeNode element){ //插入 return true; } public boolean Find(TreeNode element){ //查找 return true; } public void visted(TreeNode subTree) { subTree.setVisted(true); System.out.println("key:" + subTree.getKey() + "--name:" + subTree.getData()); } public static void main(String[] args) { BinaryTree bt = new BinaryTree(); bt.createBinTree(bt.root); System.out.println("the size of the tree is " + bt.Size()); System.out.println("the height of the tree is " + bt.Height()); System.out.println("*******先根(前序)[ABDECF]遍歷*****************"); bt.PreOrder(bt.root); System.out.println("*******中根(中序)[DBEACF]遍歷*****************"); bt.InOrder(bt.root); System.out.println("*******后根(后序)[DEBFCA]遍歷*****************"); bt.PostOrder(bt.root); }} |
結果輸出:
the size of the tree is 6
the height of the tree is 3
*******先根(前序)[ABDECF]遍歷*****************
key:1--name:rootNode(A)
key:2--name:B
key:4--name:D
key:5--name:E
key:3--name:C
key:6--name:F
*******中根(中序)[DBEACF]遍歷*****************
key:4--name:D
key:2--name:B
key:5--name:E
key:1--name:rootNode(A)
key:3--name:C
key:6--name:F
*******后根(后序)[DEBFCA]遍歷*****************
key:4--name:D
key:5--name:E
key:2--name:B
key:6--name:F
key:3--name:C
key:1--name:rootNode(A)
希望本文對學習JAVA程序設計的同學有所幫助。