動態規劃過程是:每次決策依賴于當前狀態,又隨即引起狀態的轉移。一個決策序列就是在變化的狀態中產生出來的,所以,這種多階段最優化決策解決問題的過程就稱為動態規劃。
動態規劃實際上是一類題目的總稱,并不是指某個固定的算法。動態規劃的意義就是通過采用遞推(或者分而治之)的策略,通過解決大問題的子問題從而解決整體的做法。動態規劃的核心思想是巧妙的將問題拆分成多個子問題,通過計算子問題而得到整體問題的解。而子問題又可以拆分成更多的子問題,從而用類似遞推迭代的方法解決要求的問題。問題描述:
對于序列s和t,它們之間的距離定義為:對二者其一進行幾次以下操作:1,刪除一個字符;2,插入一個字符;3,改變一個字符.每進行一次操作,計數增加1.將s和t變為相等序列的最小計數就是兩者的編輯距離(editdistance)或者叫相似度.請給出相應算法及其實現.
分析:
假設序列s和t的長度分別為m和n,兩者的編輯距離表示為edit[m][n].則對序列進行操作時存在以下幾種情況:
a,當s和t的末尾字符相等時,對末尾字符不需要進行上述定義操作中(亦即"編輯")的任何一個,也就是不需要增加計數.則滿足條件:edit[m][n]=edit[m-1][n-1].
b,當s和t的末尾字符不相等時,則需要對兩者之一的末尾進行編輯,相應的計數會增加1.
b1,對s或t的末尾進行修改,以使之與t或s相等,則此時edit[m][n]=edit[m-1][n-1]+1;
b2,刪除s末尾的元素,使s與t相等,則此時edit[m][n]=edit[m-1][n]+1;
b3,刪除t末尾的元素,使t與s相等,則此時edit[m][n]=edit[m][n-1]+1;
b4,在s的末尾添加t的尾元素,使s和t相等,則此時s的長度變為m+1,但是此時s和t的末尾元素已經相等,只需要比較s的前m個元素與t的前n-1個元素,所以滿足edit[m][n]=edit[m][n-1]+1;
b5,在t的末尾添加s的尾元素,使t和s相等,此時的情況跟b4相同,滿足edit[m][n]=edit[m-1][n]+1;
c,比較特殊的情況是,當s為空時,edit[0][n]=n;而當t為空時,edit[m][0]=m;這個很好理解,例如對于序列""和"abc",則兩者的最少操作為3,即序列""進行3次插入操作,或者序列"abc"進行3次刪除操作.
所以,以上我們不難推出編輯距離的動態規劃方程為:
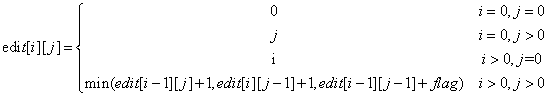
所以, 字符串編輯距離的動態規劃算法的遞歸實現可以用如下的java代碼表示:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
public static int editdistance(string a, string b) { if (a == null || b == null) { return -1; } return editdistance(a, a.length() - 1, b, b.length() - 1); } public static int editdistance(string a, int m, string b, int n) { if (m < 0 || n < 0) { return 1; } else if (a.charat(m) == b.charat(n)) { return editdistance(a, m - 1, b, n - 1); } else { return math.min(math.min(editdistance(a, m - 1, b, n) + 1, editdistance(a, m, b, n - 1) + 1), editdistance(a, m - 1, b, n - 1) + 1); } } |
update:
同時, 由編輯距離的動態規劃方程我們可以看出, edit[m][n]可以由edit[m - 1][n - 1], edit[m - 1][n], edit[m][n - 1]得出, 而如果edit是一個二維數組的話, edit[m][n]可以由它的上, 左, 左上三個位置的元素通過條件判斷得出. 亦即我們可以通過遍歷二維數組, 然后通過回溯來計算當前值.
例如對于字符串s = "sailn"和t = "failing", 對二維數組進行初始化為:
| m\n | f | a | i | l | i | n | g | |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| s | 1 | 1 | ||||||
| a | 2 | |||||||
| i | 3 | |||||||
| l | 4 | |||||||
| n | 5 |
因為s[0] = s, t[0] = f, 則s[0] != t[0], 則對應于上述二維矩陣, edit[1][1] = min(edit[0][0], edit[0][1], edit[1][0]) + 1即edit[1][1] = min(0, 1, 1) + 1即edit[1][1] = 0 + 1 = 1.
| m\n | f | a | i | l | i | n | g | |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| s | 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| a | 2 | 2 | 1 | |||||
| i | 3 | |||||||
| l | 4 | |||||||
| n | 5 |
而對于s[1] = a, t[1] = a, s[1] = t[1], 則對應于二維矩陣, edit[2][2] = edit[1][1], 所以edit[2][2] = 1. 所以按照這種規則, 將上述二維矩陣填滿則如下:
| m\n | f | a | i | l | i | n | g | |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| s | 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| a | 2 | 2 | 1 | 2 | 3 | 4 | 5 | 6 |
| i | 3 | 3 | 2 | 1 | 2 | 3 | 4 | 5 |
| l | 4 | 4 | 3 | 2 | 1 | 2 | 3 | 4 |
| n | 5 | 5 | 4 | 3 | 2 | 2 | 2 | 3 |
所以, 兩者的編輯距離為edit[m][n] = edit[5][7] = 3.
所以, 按照上述思路即動態規劃的回溯解法的java版本可以如下進行:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
public static int editdistance(string a, string b) { if (a == null || b == null) { return -1; } int[][] matrix = new int[a.length() + 1][b.length() + 1]; for (int i = 0; i < a.length() + 1; i++) { for (int j = 0; j < b.length() + 1; j++) { if (i == 0) { matrix[i][j] = j; } else if (j == 0) { matrix[i][j] = i; } else { if (a.charat(i - 1) == b.charat(j - 1)) { matrix[i][j] = matrix[i - 1][j - 1]; } else { matrix[i][j] = 1 + math.min(math.min(matrix[i - 1][j], matrix[i][j - 1]), matrix[i - 1][j - 1]); } } } } return matrix[a.length()][b.length()]; } |
總結
以上就是本文關于java動態規劃之編輯距離問題示例代碼的全部內容,希望對大家有所幫助。感興趣的朋友可以繼續參閱本站其他相關專題,如有不足之處,歡迎留言指出。
原文鏈接:http://www.cnblogs.com/littlepanpc/p/7895810.html