高度平衡的搜索二叉樹

一棵平衡樹，或是空樹，或是具有以下性質的二叉搜索樹：左子樹和右子樹都是avl樹，且左右子樹的高度之差的絕對值不超過1。 

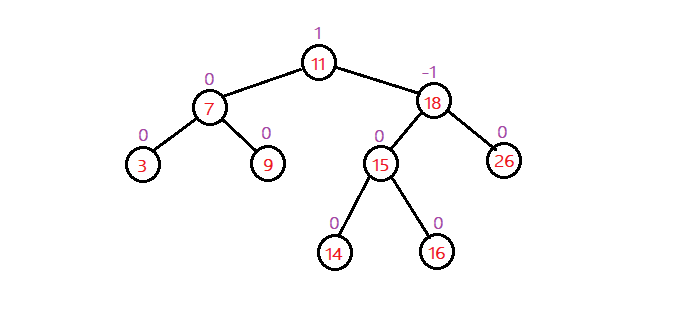
該二叉樹，根結點的右子樹高度為3，左子樹高度為2。結點上方的數(shù)字為平衡因子，因為右子樹高度比左子樹高度大1，所以根結點的平衡因子為1。

一顆平衡二叉樹，如果有n個結點，其高度可保持o(log2^n),平均搜索長度也可以保持在o(log2^n)

平衡化旋轉 

avl樹相較于普通的二叉搜索樹，自主要的就是做了平衡化處理，使得二叉樹變的平衡，高度降低。

在插入一個結點后應該沿搜索路徑將路徑上的結點平衡因子進行修改，當平衡因子大于1時，就需要進行平衡化處理。從發(fā)生不平衡的結點起，沿剛才回溯的路徑取直接下兩層的結點，如果這三個結點在一條直線上，則采用單旋轉進行平衡化，如果這三個結點位于一條折線上，則采用雙旋轉進行平衡化。

單旋轉

左單旋

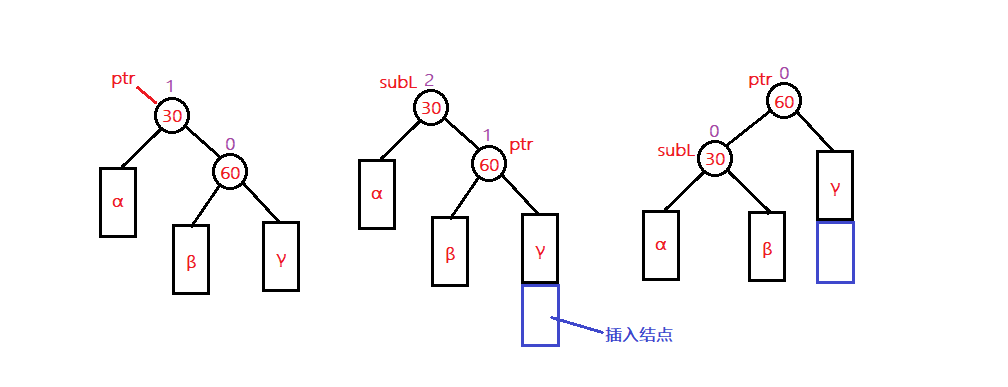
動圖演示，圖片內容可以無視，看懂操作進行了

將右子樹的左子樹鏈接到父親節(jié)點的右孩子結點，父親節(jié)點作為ptr結點的左孩子結點便完成了旋轉

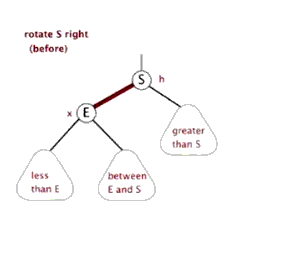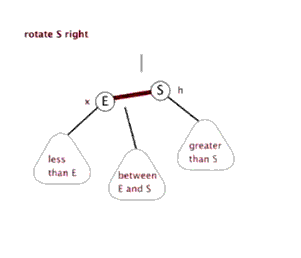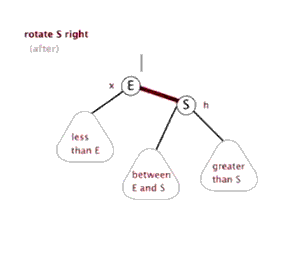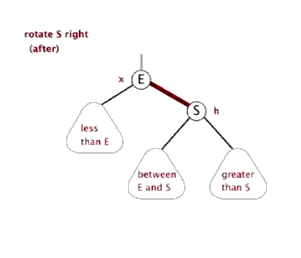
右單旋

右單旋是左單旋的鏡像旋轉. 

當前節(jié)點ptr，與父親節(jié)點和當前節(jié)點的左孩子結點位于一條直線上時，使用右單旋進行平衡。

雙旋轉

先左后右雙旋轉

當在ptr的左子樹的右子樹中插入一個結點后，造成了ptr平衡因子為-2的不平衡，將ptr向下找到當前結點的左孩子的右孩子，先進行左單旋ptr->left = subl，然后將ptr的右子樹斷開指向subr，此時便完成了旋轉，最后將平衡因子進行更新。

先右后左雙旋轉

先右單旋再左單旋，是先左后右的鏡像旋轉，這里就不做贅述了。

總結

以上就是這篇文章的全部內容了，希望本文的內容對大家的學習或者工作具有一定的參考學習價值，謝謝大家對服務器之家的支持。如果你想了解更多相關內容請查看下面相關鏈接

原文鏈接：https://blog.csdn.net/qq_43193797/article/details/85124138