function recursion(函數(shù)遞歸)
函數(shù)遞歸: 是在 一個(gè) 過(guò)程 或 函數(shù) 在其定義或說(shuō)明中有 直接 或 間接 調(diào)用自身 的一種方法
通常把一個(gè) 大型復(fù)雜的問(wèn)題 層層 傳化 為一個(gè)與 原理相似的 ,規(guī)模較小 的問(wèn)題
遞歸策略 只需 少量的程序 就可以描述出 解題過(guò)程 所需的 多次 重復(fù) 計(jì)算,大大減少了程序的代碼量
遞歸的中心思想為:
大事化小。
程序一
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
#include<stdio.h>int main(){ printf("hehe"); main();//陷入死循環(huán),但因?yàn)闂R绯觯詈髸?huì)停下來(lái) == stack overflow - 棧溢出 任何一次函數(shù)調(diào)用,它都會(huì)向內(nèi)存申請(qǐng)空間,分為三部分 棧區(qū),堆區(qū),靜態(tài)區(qū) 棧區(qū) :局部變量,函數(shù)的形參堆區(qū): 動(dòng)態(tài)開(kāi)辟的內(nèi)存 - malloc(分配內(nèi)存) and calloc(動(dòng)態(tài)內(nèi)存分配并初始化零) 靜態(tài)區(qū): 全局變量,static修飾的變量 return 0;} |
遞歸的兩個(gè)必要條件
1,存在限制條件,當(dāng)滿足這個(gè)限制條件的時(shí)候,遞歸將不再繼續(xù)
2.每次遞歸調(diào)用之后越來(lái)越接近這個(gè)條件
程序一:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
#include<stdio.h>一共調(diào)用三次 1 2 3void print(int n)// n == 123 void print(int n)n == 12 void print(int n) m == 1 { // { { if (n > 9) // if (n > 9) if (n > 9) { // { { print(n / 10);// 這里再調(diào)用 print 函數(shù) print(n / 10); print(n / 10); } // } } printf("%d ",n%10); // 最后打印3 // printf("%d ",n%10); 再打印個(gè)2 printf("%d ",n%10); 首先打印 1} // } } int main(){ unsigned int num = 0; scanf("%d",&num);//123 //遞歸 print(num);//1 2 3 return 0;} |
程序二:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
#include<stdio.h>#include<string.h>寫(xiě)法1(計(jì)數(shù)器)int my_strlen(char* str)//str指針變量,需要返回整形{ int count = 0; while (*str != '\0') { count++; str ++; } return count;}寫(xiě)法2(遞歸)int my_strlen(char* str)//str指針變量,需要返回整形{ if (*str != '\0') { return 1 + my_strlen(str + 1); } else return 0;}int main(){ char arr[] = "bit"; //int len = strlen(arr); //printf("%d\n", len); //模擬實(shí)現(xiàn)一個(gè)strlen函數(shù) int len = my_strlen(arr); printf("len = %d\n",len); return 0;} |
練習(xí)
求n的階乘
迭代與遞歸
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
#include<stdio.h>1 迭代方式 int facl(int n){ int i = 0; int ret = 1; for (i = 1; i <= n; i++) { ret = ret*i; } return ret;}遞歸方式int facl(int n){ if (n <= 1) { return 1; } else return n*facl(n - 1); 這里說(shuō)明一下思維 假設(shè) 我們 要求 10 的階乘 1x1x2x3x4x5x6x7x8x9x10 我們的 n 一開(kāi)始是 10, 10*facl(n-1) ,其實(shí) facl 函數(shù) 就是 把 10 減一,遞歸就好像是循環(huán),循環(huán)的目的,就是 得到 10每次減一的結(jié)果,直到它等于1,再讓其鏈接起來(lái), 你可以這么看 10 *(9 * (8 * (7 * ((6 * (5 * (4 *(3 * (2 * (1 * (1)))))))))) 等價(jià)于 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 * 1}int main(){ int n = 0; scanf("%d",&n); int ret = facl(n);//循環(huán)方式 printf("%d\n",ret); return 0;} |
再來(lái)道例題
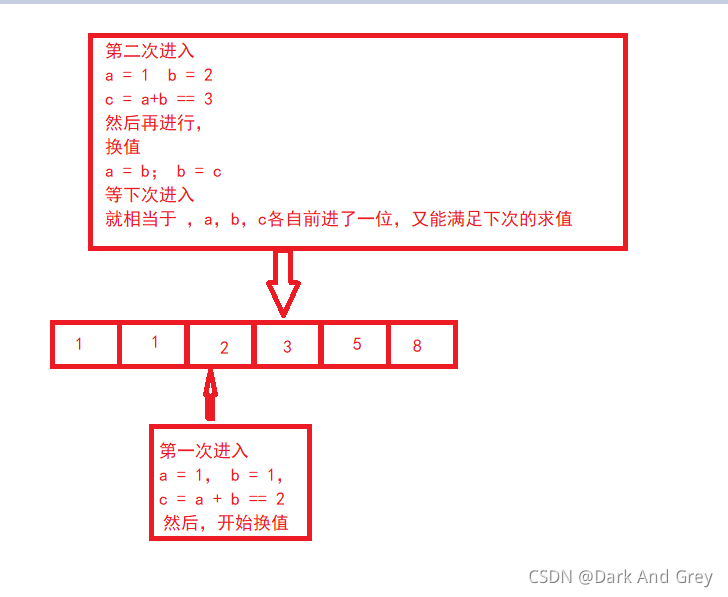
斐波那契函數(shù) 1 1 2 3 5 8 13 21
從 第三個(gè)數(shù) 開(kāi)始,該數(shù)等前面兩個(gè)數(shù)的和。
求第第n個(gè)斐波那契函數(shù)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
#include<stdio.h>這題用遞歸效率很低,很多數(shù)會(huì)重復(fù)計(jì)算int fib(int n){ if (n <= 2) return 1; else return fib(n - 1)+fib(n - 2);// 因?yàn)?函數(shù) 每得到一個(gè)數(shù),就需要將得到的數(shù)進(jìn)行分解成 2個(gè) 部分}2迭代(循環(huán))方式(簡(jiǎn)單加法)效率更高int fib(int n){ int a = 1; int b = 1; int c = 1; while (n>2)// { c = a + b; a = b; b = c; n--; } return c;}int main(){ int n = 0; scanf("%d",&n); int ret = fib(n); printf("%d\n",ret); return 0;} |
到此這篇關(guān)于C語(yǔ)言 function recursion函數(shù)遞歸詳解的文章就介紹到這了,更多相關(guān)C語(yǔ)言 函數(shù)遞歸內(nèi)容請(qǐng)搜索服務(wù)器之家以前的文章或繼續(xù)瀏覽下面的相關(guān)文章希望大家以后多多支持服務(wù)器之家!
原文鏈接:https://blog.csdn.net/DarkAndGrey/article/details/120605939