1、浮點數(shù)

浮點數(shù)是C++的第二組基本類型，它能夠表示帶小數(shù)部分的數(shù)字。不僅如此，浮點數(shù)的范圍也比int更大，可以表示更大范圍的數(shù)字。

我們都知道在計算機(jī)當(dāng)中，所有數(shù)據(jù)本質(zhì)上都是轉(zhuǎn)化成二進(jìn)制存儲的。整數(shù)很簡單，存儲的就是轉(zhuǎn)化成二進(jìn)制之后的01串，那么浮點數(shù)又是如何存儲的呢？

很容易猜到的是浮點數(shù)存儲的結(jié)果也是二進(jìn)制，但相比于整型直接轉(zhuǎn)化成二進(jìn)制要復(fù)雜一些。

它需要先表示成下面這行式子：

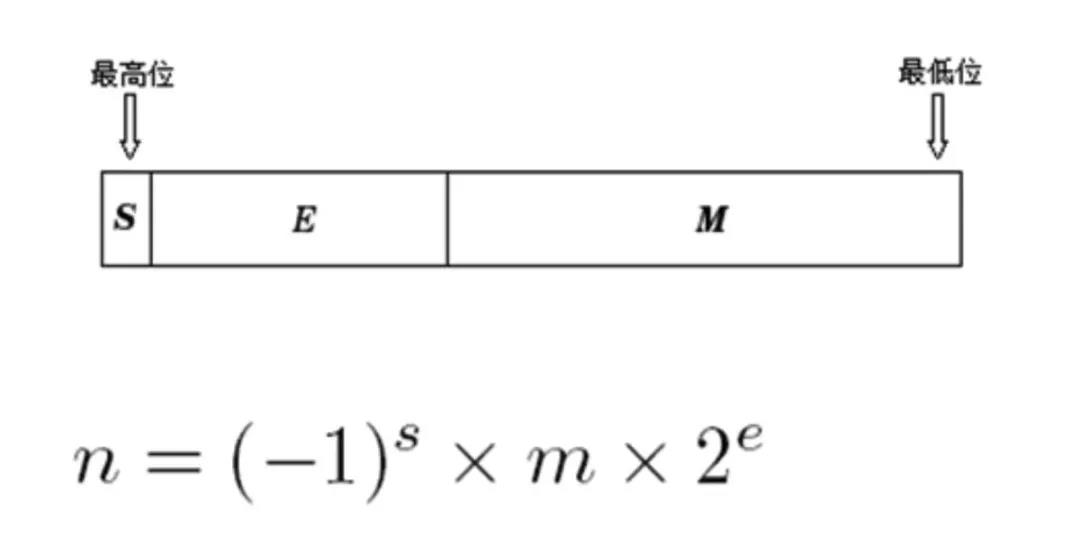
這里的n即我們要存儲的浮點數(shù)，s表示符號位，m是尾數(shù)，而e則是階數(shù)。

符號位很好理解，它和整型當(dāng)中的符號位一樣，0表示正數(shù)，1表示負(fù)數(shù)。m表示尾數(shù)，。我們這么看很抽象，來看一個例子，比如3.0，轉(zhuǎn)化成二進(jìn)制是，相當(dāng)于。那么，。

我們了解了浮點數(shù)的表示方式，那么它又是如何存儲在計算機(jī)當(dāng)中的呢？這需要我們進(jìn)一步地剖析其中的細(xì)節(jié)。

2、關(guān)于m

首先是m，m被定義成一個大于等于1，小于2的小數(shù)。我們可以簡單寫成1.xx，其中xx表示的就是小數(shù)的部分。

既然它總是大于等于1，小于2的，那么它的個位一定是1，我們就可以將它省略，僅僅看之后小數(shù)的部分。小數(shù)的部分，我們同樣使用二進(jìn)制來逼近。比如0.625，可以表示成0.5 + 0.125，即，表示成二進(jìn)制就是，只不過這里它的最高位是從-1開始的。

以32位的浮點數(shù)為例，除去1位表示符號，8位表示階數(shù)之后，還有23位留給m。由于我們舍掉了小數(shù)點之前的1，所以我們的階數(shù)是從-1開始的，理論上等價于24個二進(jìn)制位。

3、關(guān)于e

在浮點數(shù)存儲當(dāng)中，e是一個無符號整數(shù)。以32位浮點數(shù)為例，e一共有8位，可以表示0-255。

但e是可以為負(fù)數(shù)的，根據(jù)IEEE 754的規(guī)定，e的真實值必須再減去一個中間數(shù)。對于8位的e，它的中間數(shù)是127。比如e的實際值是10，但是存儲的時候需要存儲成127+10=137。

除此之外，e還有另外三種情況：

• e不全為0，或全為1時，采用上述的規(guī)則表示
• e全為0時，e等于1-127，有效數(shù)字m不再默認(rèn)加上1，這樣是為了還原0.xxx的小數(shù)，以及接近于0的數(shù)
• e全為1時，如果有效數(shù)字m全為0，表示無窮大，如果m不全為0，表示nan（not a number）

關(guān)于e的規(guī)則看起來有些復(fù)雜，初看覺得有些難以理解，為什么要用減去中間值的設(shè)計，而不用符號位？后來仔細(xì)思考了一下才發(fā)現(xiàn)，如果引入符號位很難區(qū)分0.xxx以及e就是等于0的情況，雖然也可以特判處理，但就沒有現(xiàn)在這樣優(yōu)雅了。

覺得上文看不懂的小伙伴可以直接略過這段，畢竟這個是浮點數(shù)的實現(xiàn)原理，算是很底層的內(nèi)容了，C++ primer上對于這部分也沒有過多闡述。

4、浮點數(shù)的使用

C++當(dāng)中有兩種浮點數(shù)的書寫方式，第一種是使用常規(guī)的小數(shù)點表示法：

另外一種寫法是科學(xué)記數(shù)法，寫成：

2.45e8表示，e之后可以跟正數(shù)也可以跟負(fù)數(shù)，但數(shù)字當(dāng)中不能有空格。

5、浮點數(shù)類型

和C語言一樣，C++也有三種浮點數(shù)類型：float,double和long double。和整型一樣，這三種類型都是浮點數(shù)，只不過表示的范圍不同。

浮點數(shù)的范圍有兩個部分綜合決定，一個部分是有效數(shù)字。比如14179是5位有效數(shù)字，而14000只有兩位，因為后面三個0都是填充位，有效數(shù)字的位數(shù)不依賴小數(shù)點的位置。C++當(dāng)中要求，float通常表示7位有效數(shù)字，double通常16位位，而long double至少和double一樣。

另外，它們能夠表達(dá)的指數(shù)范圍至少是-37到37。一般來說，float一共是4個字節(jié)32位，而double是8個字節(jié)64位，當(dāng)然這也取決于具體的運(yùn)行環(huán)境。

6、注意事項

關(guān)于浮點數(shù)的使用有幾點注意事項，千萬要注意。

• cout輸出浮點數(shù)會刪除結(jié)尾的0
• 書寫浮點數(shù)常量時默認(rèn)為double類型，如果需要強(qiáng)制表示為float類型，請在結(jié)尾加上后綴f或者F，如：2.34f
• 由于浮點數(shù)有精度，不能直接判斷兩個浮點數(shù)是否相等，很有可能得不到預(yù)期結(jié)果，正確的做法是判斷精度范圍，

如：

判斷兩個浮點數(shù)a和b是否相等，等價于兩者的差的絕對值小于某一個精度。

范圍問題，如運(yùn)行下列代碼將得到錯誤的結(jié)果：

輸出的結(jié)果將是0，因為2.3e22是一個小數(shù)點左邊有23位的數(shù)字，加上1之后，就是在第23位加上1。但是float類型只能表示數(shù)字中的前6位或者前7位，表示不了這么高的精度，因此這個+1的操作完全沒有生效。

這個問題是一個大坑，一不小心就會中招，千萬要小心。

到此這篇關(guān)于C++浮點數(shù)類型詳情的文章就介紹到這了,更多相關(guān)C++浮點數(shù)類型內(nèi)容請搜索服務(wù)器之家以前的文章或繼續(xù)瀏覽下面的相關(guān)文章希望大家以后多多支持服務(wù)器之家！

注：文章轉(zhuǎn)自微信公眾號：Coder梁（ID：Coder_LT）