一.定義
逆波蘭式,又稱后綴表達式,指的是操作符在其所控制的操作數后面的表達式。
舉個例子,1 + 2 * 3 - 4這個表達式是我們熟悉的中綴表達式,那么其所對應的后綴表達式為:1 2 3 * + 4 -。
再來個復雜的例子:1 * (2 + 3) / 5 - 4 / 2其對應的后綴表達式為:1 2 3 + * 5 / 4 2 / -(其中括號由于只是提升表達式優先級的作用,因此不放入后綴表達式中)。
二.逆波蘭式的意義
為什么要將看似簡單的中綴表達式轉換為復雜的逆波蘭式,原因就在于這個簡單是相對我們人類的思維結構來說的,對計算機而言中序表達式是非常復雜的結構。相對的,逆波蘭式在計算機看來卻是比較簡單易懂的結構。因為計算機普遍采用的內存結構是棧式結構,它執行先進后出的順序。
三.逆波蘭式的實現
1.方法
(1)中綴表達式轉化為后綴表達式
對于給出的中綴表達式,如何將其轉化為后綴表達式呢?
第一,若遇到操作數則直接輸出/存儲。
第二,遇到操作符,若此時棧為空或者操作符優先級高于棧頂,則入棧。
第三,若操作符的優先級低于或者等于棧頂,則出棧直至棧空或者優先級低于該操作符。
第四,遇到"(",其后的所有操作符(直至遇到")")按上述操作入棧或出棧;當遇到")‘時,將"("頂上的所有操作符出棧。
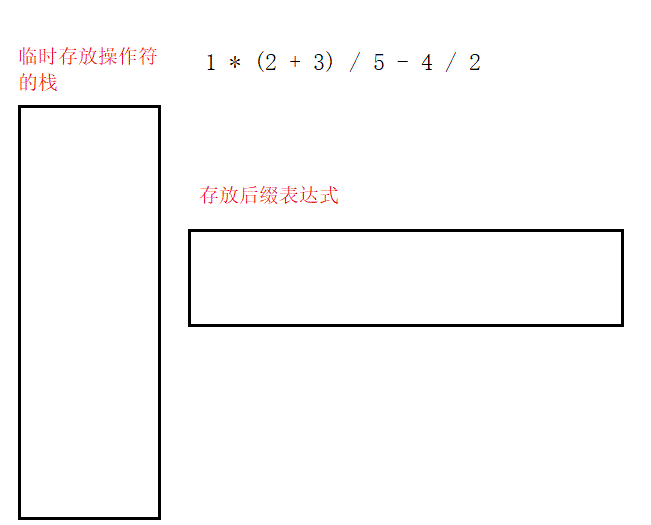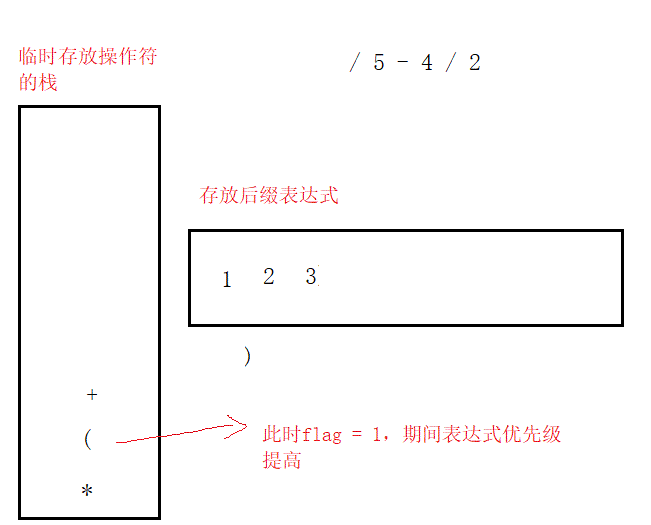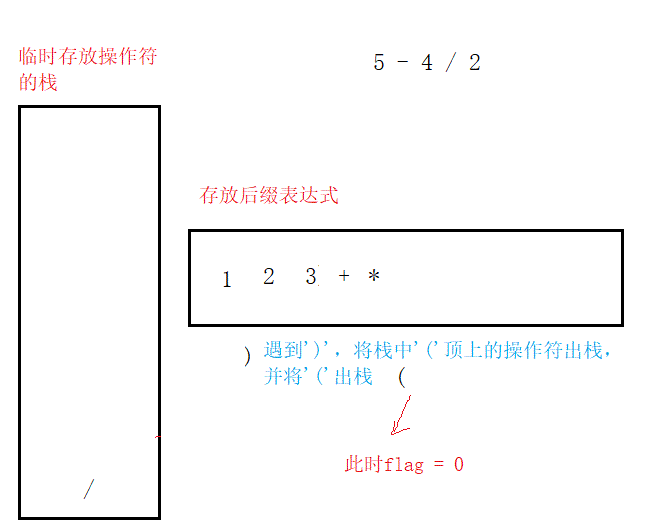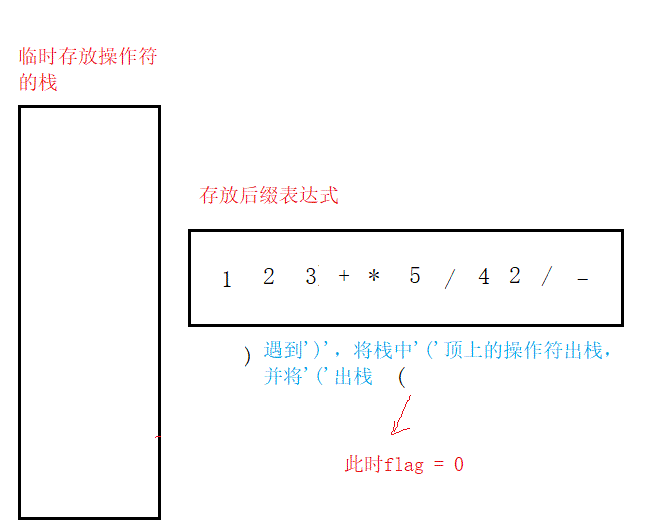
(2)由后綴表達式計算結果
第一,遇到操作數則入棧。
第二,遇到操作符則將棧頂的兩個操作數出棧,其中第一個數為右操作數,第二個數為左操作數。
第三,計算結果并將計算的結果入棧。
第四,最后棧頂的結果即為所計算的結果。

2.代碼實現
#include <iostream>
#include <string>
#include <stack>
#include <vector>
using namespace std;
string trans(string& s)
{
string operand;
stack<char> Operator;
int flag = 0;//記錄括號優先級
for (const auto& e : s)
{
if (e == "(")
{
Operator.push(e);
flag = 1;
continue;
}
if (e == ")")
{
flag = 0;
while (Operator.top() != "(")
{
operand.push_back(Operator.top());
Operator.pop();
}
Operator.pop();
continue;
}
//操作符
if (e == "+" || e == "-" || e == "*" || e == "/")
{
if (flag == 1)
{
if (Operator.top() == "(")
{
Operator.push(e);
}
else if ((e == "*" || e == "/") && (Operator.top() == "+" || Operator.top() == "-"))
{
Operator.push(e);
}
else//操作符的優先級低于或等于棧頂操作符則出棧,直至遇到"("
{
while (Operator.top() != "(")
{
operand.push_back(Operator.top());
Operator.pop();
}
Operator.push(e);
}
}
else if (Operator.empty())//棧空就入棧
{
Operator.push(e);
}
//操作符的優先級高于棧頂操作符,入棧
else if ((e == "*" || e == "/") && (Operator.top() == "+" || Operator.top() == "-"))
{
Operator.push(e);
}
else//操作符的優先級低于或等于棧頂操作符則出棧,直至棧空或者優先級高于棧頂操作符
{
while (!Operator.empty())
{
operand.push_back(Operator.top());
Operator.pop();
}
Operator.push(e);
}
}
//操作數
else
{
operand.push_back(e);
}
}
while (!Operator.empty())
{
operand.push_back(Operator.top());
Operator.pop();
}
return operand;
}
int evalRPN(const string& s)
{
stack<char> operand;
int left = 0, right = 0;
for (const auto& e : s)
{
if (e == "+" || e == "-" || e == "*" || e == "/")
{
switch (e)
{
case "+":
right = operand.top();
operand.pop();
left = operand.top();
operand.pop();
operand.push(left + right);
break;
case "-":
right = operand.top();
operand.pop();
left = operand.top();
operand.pop();
operand.push(left - right);
break;
case "*":
right = operand.top();
operand.pop();
left = operand.top();
operand.pop();
operand.push(left * right);
break;
case "/":
right = operand.top();
operand.pop();
left = operand.top();
operand.pop();
operand.push(left / right);
break;
}
}
else//操作數
{
operand.push(e - "0");
}
}
return operand.top();
}
int RPN(const string& str)
{
//1.中綴表達式轉化為后綴表達式
string s(str);
s = trans(s);
//2.后綴表達式計算答案
return evalRPN(s);
}
int main()
{
string s("1*(2*3+5)/5-4/2");
int ret = RPN(s);
cout << "ret:" << ret << endl;
return 0;
}
結果:

到此這篇關于C++棧實現逆波蘭式的應用的文章就介紹到這了,更多相關C++ 逆波蘭式內容請搜索服務器之家以前的文章或繼續瀏覽下面的相關文章希望大家以后多多支持服務器之家!
原文鏈接:https://blog.csdn.net/love_guanghui/article/details/121526718