漢諾塔的游戲規則:

有三根金剛石柱子A、B、C,在A柱子上從下往上按照大小依次減小的順序摞著64片黃金環。大梵天命令婆羅門把環從下面開始按大小順序重新擺放在另一根柱子上。并且規定,在任何一個柱子上,小環上不能放大環,在三根柱子之間一次只能移動一個環。
即將A柱子上全部的環通過C柱子(C柱子作為中介)移動到B柱子上
當A只有一個環的時候:
A->B
當A只有兩個環的時候:
A->C A->B C->B
當A只有三個環的時候:
A->B A->C B->C A->B C->A C->B A->B
思路:
- 1、將 n-1個環先放到C柱子上
- 2、將A柱子上的最后一個環移動到B柱子上
- 3、將n-1個環從C柱子移動到B柱子上
當n=1時:
1、將0個環先放到C柱子上
2、將A柱子上的最后一個環移動到B柱子上:A->B
3、將0個環從C柱子移動到B柱子上
當n=2時:
1、將1個環先放到B柱子上:A->C
2、將A柱子上的最后一個環移動到B柱子上:A->B
3、將1個環從C柱子移動到B柱子上:C->B
當n=3時:
1、將2個環先放到C柱子上:使用遞歸將2個環放到C上,因為A柱子的最后一個環是最大的因此可以先不理會,遞歸重復當n=2時的步驟,不過是從將2個環從A放到B上改為將2個環從A放到C上了
2、將A柱子上的最后一個環移動到B柱子上:A->B
3、將2個環從C柱子移動到B柱子上:使用遞歸將2個環從C柱子移動到B柱子上,此時B柱子上已經有了最大的一個環因此可以不用再理會了,遞歸重復當n=2的步驟,不過是從將2個環從A放到B上改為將2個環從C放到B上了
當n=4時:
1、將3個環先放到C柱子上:遞歸重復n=3的步驟,不過是從將3個環從A放到B上改為將3個環從A放到C上了
2、將A柱子上的最后一個環移動到B柱子上:A->B
3、將3個環從C柱子移動到B柱子上:遞歸重復當n=3的步驟,不過是從將3個環從A放到B上改為將3個環從C放到B上了
見代碼
#include <stdio.h>
void hanoi(int num, char sou, char tar, char aux) {
//統計移動次數
static int i = 1;
//如果圓盤數量僅有 1 個,則直接從起始柱移動到目標柱
if (num == 1) {
printf("第%2d次:從 %c 移動至 %c\n", i, sou, tar);
i++;
}
else {
//遞歸調用 hanoi() 函數,將 num-1 個圓盤從起始柱移動到輔助柱上
hanoi(num - 1, sou, aux, tar);
//將起始柱上剩余的最后一個大圓盤移動到目標柱上
printf("第%2d次:從 %c 移動至 %c\n", i, sou, tar);
i++;
//遞歸調用 hanoi() 函數,將輔助柱上的 num-1 圓盤移動到目標柱上
hanoi(num - 1, aux, tar, sou);
}
}
int main()
{
int n = 0;
scanf("%d", &n);
//起始柱、目標柱、輔助柱分別用 A、B、C 表示
hanoi(n, 'A', 'B', 'C');
return 0;
}
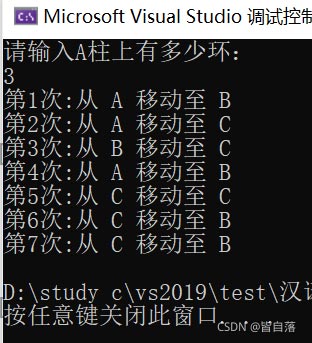
運行截圖總結


以上就是本文的全部內容,希望對大家的學習有所幫助,也希望大家多多支持服務器之家。
原文鏈接:https://blog.csdn.net/qq_61514490/article/details/121605669